自动搬运

查看原文

来自洛谷，原作者为

	hzf **

搬运于2025-08-24 21:42:28，当前版本为作者最后更新于2017-12-10 11:40:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

更良好的阅读体验，在博客食用更佳~QAQ

题意：

有一块n*n的区域，给你一些FJ的点和Bob的点，现在让你添加一个点，使FJ的点构成的正方形最大（不能添加在Bob的点上）。

样例解释：

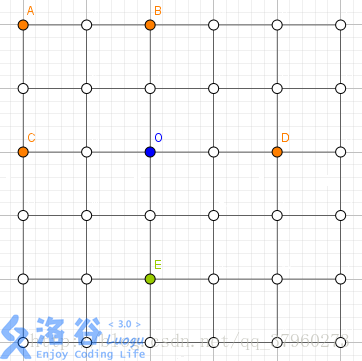
样例输入为一个$6 \times 6$的地图，橙色点为FJ的奶牛，绿色点为Bob的奶牛，白色点为未占用区域，能够成的最大正方形为ABOC，面积为$2x2=4$。

其实添加一个点能够成的最大的正方形是BCED，面积为$2 \times 2+2 \times 2=8$，可是点E是Bob的奶牛，两头奶牛不能放在同一个点上，所以只能选择前一种方案，输出4。

题解

一般来说，想要构造正方形，枚举边有两种情况，一种上方，一种下方，如图：

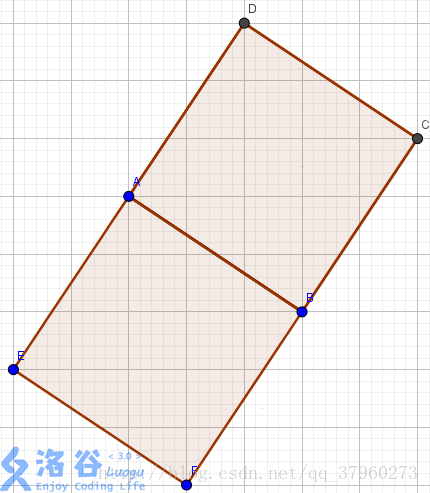
枚举A，B两点的坐标，若是以A，B为正方形的边长，会枚举出两个正方形， 正方形ABCD 和 正方形ABFE ，这时就不利于我们进行很好的计算。若是以A，B为正方形的对角线呢？

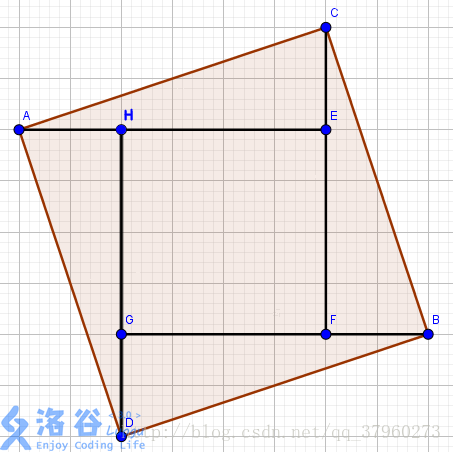
如图，我们枚举A，B两点为 正方形ACBD 的对角线，只能画出唯一一个正方形，我们的最基本的目的达到了——保证正方形的唯一性。

接下来，知道了A，B两点的坐标，如何得出C，D两点的坐标呢？

通过观察，我们发现，

A，B横坐标差=HG=HE=AE-AH；

A，B纵坐标差=AE+BF=AE+AH；

两式相加减后得：

2DH=(A，B纵坐标差)+(A，B横坐标差)；

2AH=(A，B纵坐标差)-(A，B横坐标差)；

所以

DH=CF=((A，B纵坐标差)+(A，B横坐标差))/2；

AH=BF=((A，B纵坐标差)-(A，B横坐标差))/2；

D点坐标即为(AX+DH,AY+AH);

C点坐标即为(BX-CF,BY-BF);

值得注意的是，现在C，D的坐标还没定下来，因为有可能出现另一种情况：

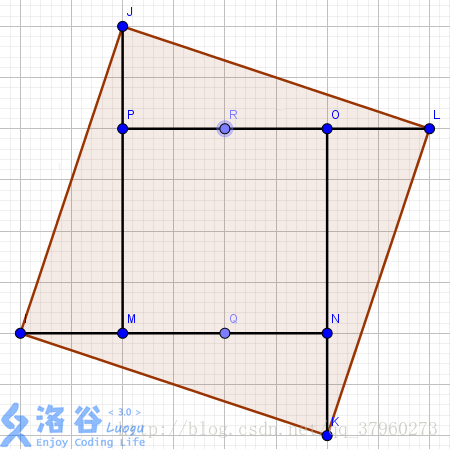
即将上一个图轴对称过来，这时按刚刚的方程得出来的是Q，R两点，并不是我们想要的正方形，这时只需要将方程变动一下就好了：

L点坐标即为(JX+JP,JY+PL);

I点坐标即为(KX-NK,KY-NI);

正方形构造好了，接下来就只需要统计最大的就行了，因为FJ可以往点阵里添加一个点，所以只需要四个顶点中有>=3个点就能构造成。

最后贴上通俗易懂的代码：

#include<bits/stdc++.h>
#define F(i,j,n) for(register int i=j;i<=n;i++)
using namespace std;
int n,s=0,ans=0,a1,a2,a3,a4,a5,a6,a7,a8;
char a[105][105];
inline int read(){
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=10*x+ch-'0';ch=getchar();}
	return x*f;
}
inline int solve(int Sum,int Minus,char Kind){
	if(Kind=='+')
		return (Sum+Minus)>>1;
	if(Kind=='-')
		return (Sum-Minus)>>1;
}
int main(){
	n=read();
	F(i,1,n)
		scanf("%s",a[i]+1);
	F(i,1,n)/*枚举右下的点的横坐标*/
		F(j,1,n)/*枚举右下的点的纵坐标*/
			F(k,1,i)/*枚举左上的点的横坐标*/
				F(tt,1,j){/*枚举左上的点的纵坐标*/
					if(a[i][j]=='B'||a[k][tt]=='B')/*如果有Bob的牛就continue*/
						continue;
					int Sum=max(i-k,j-tt),Minus=min(i-k,j-tt);
					if((Sum&1)!=(Minus&1))/*细节！判断奇偶性是否相同*/ 
						continue;
					int px=solve(Sum,Minus,'+'),py=solve(Sum,Minus,'-');/*计算出两式和与差*/
					int p=k+px,q1=tt+py,u=i-px,v=j-py;/*得出剩下两点*/
					if(((p-u)*(p-u)+(q1-v)*(q1-v))!=(Sum*Sum+Minus*Minus))/*考虑轴对称的情况*/
						p=k+py,q1=tt+px,u=i-py,v=j-px;
					if(p>=1&&q1>=1&&u>=1&&v>=1&&p<=n&&q1<=n&&u<=n&&v<=n)
						if(a[i][j]!='B'&&a[k][tt]!='B'&&a[p][q1]!='B'&&a[u][v]!='B'){
							s=0;
							if(a[i][j]=='J')
								s++;
							if(a[k][tt]=='J')
								s++;
							if(a[p][q1]=='J')
								s++;
							if(a[u][v]=='J')
								s++;
							if(s>=3&&px*px+py*py>ans){
								ans=px*px+py*py;
								a1=i;a2=j;a3=u;a4=v;
								a5=k;a6=tt;a7=p;a8=q1;
							}
						}
				}
	printf("%d\n",ans);
	//printf("\n\n%d %d\n%d %d\n%d %d\n%d %d\n",a1,a2,a3,a4,a5,a6,a7,a8);
	return 0;
}