自动搬运

查看原文

来自洛谷，原作者为

	Trinity **

搬运于2025-08-24 21:41:59，当前版本为作者最后更新于2018-07-13 19:48:47，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目 ：P2822 组合数问题 2016 提高组 T1 & 组合数求解方法总结

题目描述

组合数$C^m_n$表示的是从n个物品中选出m个物品的方案数。举个例子,从$(1,2,3)$三个物品中选择两个物品可以有$(1,2),(1,3),(2,3)$这三种选择方法。 根据组合数的定义，我们可以给出计算组合数的一般公式：
$C^m_n=\frac{n!}{m!(n-m)!}$ 其中$n!=1\times2\times\cdots\times n$特别地，定义$0!=1$。
小葱想知道如果给定$n,m$和$k$对于所有的$0≤i≤n,0≤j≤min(i,m)$,有多少对 $(i,j)$满足$C_i^j$是$k$的倍数。

分析

1.看一波数据范围，发现事情并没有这么简单 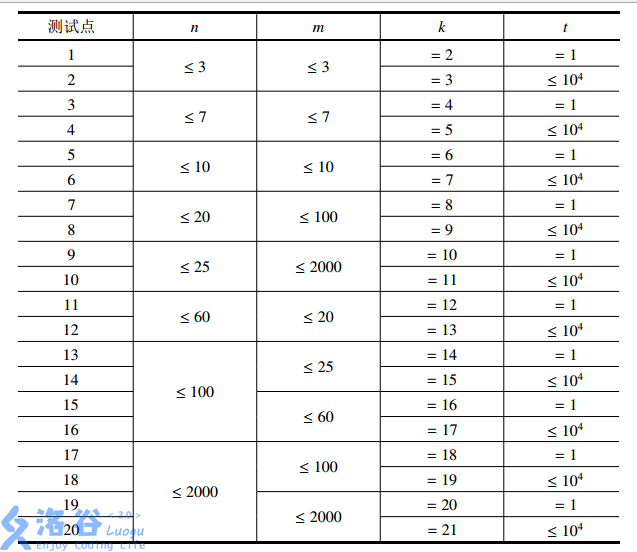用公式不可能过。
2.可以利用多组数据，加快组合数的求解。
3.对数据取模可以防止溢出和TLE

解题过程&题解

$1$ . $30$分 暴力(套公式法，千万别像我一样思维简单)
对于小范围数据可以直接打阶乘和组合数公式，对于稍稍大的可以打出阶乘表( 下方未实现 ),但是对于超过long long范围的数据无能为力

LL t,k,n,m,ans;
inline LL ck(LL x)//开long long可以算更多
{
  if(x==0)return 1;
  int sum=1;
  for(int i=1;i<=x;i++)sum*=i;
  return sum;
}
inline LL C(LL n,LL m)
{
  return ck(n)/(ck(m)*ck(n-m));//组合数公式
}
int main()
{
  t=read(),k=read();
  while(t--)
  {
    ans=0;
    n=read(),m=read();
    for(LL i=0;i<=n;i++)
      for(int j=0;j<=min(m,i);j++)
        if(C(i,j)%k==0)ans++;//统计
      printf("%lld\n",ans);
  }
  return 0;
}

$2$ . $70$分 组合数递推法
针对大多数仅仅是利用组合数求解问题的题目运用递推法打表，不仅方便，而且可以稳稳地控制复杂度，对于需要多次引用组合数的题目效果极佳：
基于组合数公理性质：$C^m_n=C^{n-m}_n$ （请大家务必记住此公式，由此在考场上灵活使用） 推得：$C^m_n=C^{m-1}_{n-1}+C^m_{n-1}$

**感谢各位大佬指出我的问题，确实当年的递推公式写错了，完全在于当时的我对其理解不清晰，特在高二退役后8个月修正 **

由这个递推公式就可以熟练的写出组合数代码，但要注意初始化:

$C^0_0=0$
$C^i_0=C^1_0=C^1_1=1$ ( $i$为自然数 )

同时，把表打出来后，我们会发现———这就是杨辉三角，这个三角可以解决很多问题，记住打印三角的方法也可以打出组合数。

inline void build()//记得加入main函数，数组范围要开够，我就是在此RE。
{
  c[0][0]=1;
  c[1][0]=c[1][1]=1;//如上初始化，绝对绝对不能忘记或错，结合常识。
  for(int i=2;i<=2000;i++)
  {
    c[i][0]=1;
    for(int j=1;j<=2000;j++)//这不是此方法能承受的最大范围，打出题目要求的即可。
      c[i][j]=c[i-1][j-1]+c[i-1][j];//递推公式。
  }
}
inline void solve()
{
  build();
  t=read(),k=read();
  while(t--)
  {
    ans=0;
    n=read(),m=read();
    for(int i=0;i<=n;i++)
      for(int j=0;j<=my_min(i,m);j++)
        if(c[i][j]%k==0)ans++;
    printf("%lld\n",ans);
  }
}

$3$ . 90分 本题的特殊优化———取模大法（我没想出来，看了题解才恍然大悟 ）
三部一取模，有效的防止溢出，还减少了递推的次数，但你会问为什么取模能保证递推式的正确性，而不加大位运算的时间呢？
显然，我们带几个数字试一试，可以初步确定：
$ (C^m_n)\bmod k=(C^{m-1}_{n-1})\bmod k+(C^{m}_{n-1})\bmod k$
完全正确。
但可惜的是，本题数据惊人，还是会TLE两个点，还需要继续优化和卡常。

inline void build()
{
  c[0][0]=1;
  c[1][0]=c[1][1]=1;
  for(int i=2;i<=2000;i++)
  {
    c[i][0]=1;
    for(int j=1;j<=2000;j++)
      c[i][j]=(c[i-1][j-1]%k+c[i-1][j]%k)%k;//重中之重，绝不能盲目地模。
  }
}

$4$ . 95分 本人瞎搞出的玄学优化———先模再说
$mod$是高级运算（ 可能运用了位运算 ）比四则运算更耗时。我们在建立组合数表的时候先判断元素是否满足整除条件，在主函数计数时可以减小计算量。（时间消耗）
不信，来看

inline void build()
{
  c[0][0]=1;
  c[1][0]=c[1][1]=1;
  for(int i=2;i<=2000;i++)
  {
    c[i][0]=1;
    for(int j=1;j<=2000;j++)
    {
      c[i][j]=(c[i-1][j-1]+c[i-1][j])%k;
      if(c[i][j]%k==0)s[i][j]=1;//先记一下，如果已经满足条件，就标记一下，省去了更多的计算。
    }
  }
}
inline void solve()
{
  t=read(),k=read();
  build();
  while(t--)
  {
    ans=0;
    n=read(),m=read();
    for(int i=0;i<=n;i++)
      for(int j=0;j<=my_min(i,m);j++)
        ans+=s[i][j];
    printf("%lld\n",ans);
  }
}

$5$ .$100$分 前缀和+递推打表
大家知道，即使打过表，算法的复杂度其实还多的一维，也就是这反复查询让人难以想到，使得我死死卡在95分一整天，才又翻了题解。
前缀和，有效减少查询统计时的复杂度，每一次查询$O(n)$降到$O(1),绝对过的了 记住：上加左 减左上 加自己（ by 巨佬[Arthur_L](https://www.luogu.org/blog/user42796/solution-p2822) ) $ans[i][j]=ans[i][j-1]+ans[i-1][j]-ans[i-1][j-1]$

inline void build()
{
  c[0][0]=1;
  c[1][0]=c[1][1]=1;
  for(int i=2;i<=2000;i++)
  {
    c[i][0]=1;
    for(int j=1;j<=i;j++)
    {
      c[i][j]=(c[i-1][j-1]+c[i-1][j])%k;
      ans[i][j]=ans[i-1][j]+ans[i][j-1]-ans[i-1][j-1];//前缀和。
      if(!c[i][j])ans[i][j]++;//如果满足结论，计数加一。(有没有感觉很像我的玄学优化）
    }
    ans[i][i+1]=ans[i][i];//继承。
  }
}
inline void solve()
{
  t=read(),k=read();
  build();
  while(t--)
  {
    n=read(),m=read();
    if(m>n)printf("%lld\n",ans[n][n]);//如果m>n,ans只会达到n，只需输出ans[n,n]就可以了。
    else printf("%lld\n",ans[n][m]);
  }
}

总结

1.需掌握组合数的基本两种求解方法(通项公式，递推公式），根据数据范围选定方法。
2.结合数据范围找到优化方法，无论是取模还是自己的玄学优化都尝试一下.(建议取模输出的题，绝！对！不！要！乱！模！，既费时又易错)
3.掌握前缀和，利用前缀和对降维的作用。

最后，我的题解又臭又长，主要是总结求解组合数的各种方法，其次分享一下自己的优化(卡常)技巧，谢谢大家的更正。