自动搬运

查看原文

来自洛谷，原作者为

	logfk 不是哥们，退役了还看啊

搬运于2025-08-24 21:41:52，当前版本为作者最后更新于2021-05-05 08:54:31，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

前置知识

tarjan

缩点

题意

有 $n$个点，$m$条边，每个点有一个点权，求选择某些点后，使得每个点始终能够到达，且选择的点权和最小，并求出点权和最小的方案数。

分析

为什么要缩点？

题目中要求最少的保安，而一个保安就可以控制一个环，所以可以用缩点求出最少的保安数。

如何理解始终？

就是说，你在处理一个紧急事件后，仍旧能够处理其他所有的紧急事件，讨论区中有一个比较有趣的问题，是对样例的错误分析，我们把样例搞出来。

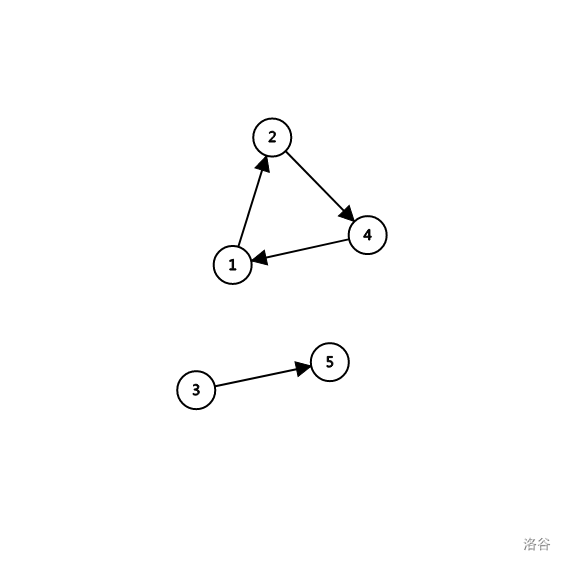
疑问是：选择 $3$、$4$后图就是能够到达的，但是出现了一个问题：$3$处理了 $5$之后，这个保安便不能再回到 $3$了，所以说没有满足始终这个约束条件。

所以我们得出，缩点后，每个点的值（或者环中的最小值）的总和便是我们要求的最小点权和，至于方案数，每个环中可能有多个最小值，使用乘法原理解决即可。

代码部分

#include<iostream>
#include<vector>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;
vector <int>a[10010];
int sta[10010],top=0,flag[10010],num,tot,col[10010],ss[10010];
int ans,va[10010],dfn[10010],low[10010],ans1=1,mm[10010],nn[10010],sc[10010];
void tarjan(int x)//标准tarjan缩点
{
    sta[++top]=x;
    flag[x]=1;
    dfn[x]=low[x]=++num;
    for(int i=0;i<a[x].size();i++)
    {
        int y=a[x][i];
        if(!dfn[y])
        {
            tarjan(y);
            low[x]=min(low[x],low[y]);
        }
        else
        {
            if(flag[y])
            {
                low[x]=min(low[x],dfn[y]);
            }
        }
    }
    if(dfn[x]==low[x])
    {
        tot++;
        while(sta[top+1]!=x)
        {
            col[sta[top]]=tot;
            ss[tot]+=va[sta[top]];
            flag[sta[top--]]=0;
        }
    }
}
int read()
{
	char c=getchar();
	int x=0;
	while(c<'0'||c>'9') c=getchar();
	while(c>='0'&&c<='9')
	{
		x=x*10+c-'0';
		c=getchar();
	}
	return x;
}
int main()
{
	memset(mm,0x3f,sizeof(mm));
    int n,m,u,v;
    n=read();
    for(int i=1;i<=n;i++)
    {
        va[i]=read();
    }
    m=read();
    for(int i=1;i<=m;i++)
    {
    	u=read(),v=read();
        a[u].push_back(v);
    }
    for(int i=1;i<=n;i++)
    {
        if(!dfn[i]) tarjan(i);
    }
    for(int i=1;i<=n;i++)//把点或者环的最小值处理出来，并且统计最小值的数量
    {
    	if(!sc[col[i]])
    	{
    		sc[col[i]]=col[i];
    	}
    	if(va[i]<mm[col[i]])
    	{
    		mm[col[i]]=va[i];
    		nn[col[i]]=1;
    	}
    	else
    	{
    		if(va[i]==mm[col[i]])
    		{
    			nn[col[i]]++;
    		}
    	}
    }
    for(int i=1;i<=n;i++)//一加一乘，解决战斗
    {
    	if(sc[i])
    	{
    		ans+=mm[sc[i]];
    		ans1*=nn[sc[i]];
    	}
    }
	cout<<ans<<" "<<ans1<<endl;
}

蒟蒻实力不足，有问题欢迎指出