[NOI2009] 植物大战僵尸

0
15011418730 LV 7 @ 2025-8-24 21:41:48
自动搬运

查看原文

来自洛谷，原作者为

longlongzhu123
**

搬运于2025-08-24 21:41:48，当前版本为作者最后更新于2018-12-23 11:34:21，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

解法：网络流 - 最大权闭合子图 $\times$ 拓扑排序

感觉大家的题解都没有讲得很清楚呢。

鉴于大家可能会以这道题作为 最大权闭合子图 的入门题，我就在这里给大家讲一些有关的概念，帮助大家快速入门吧！
- 如果你早就知道最大权闭合子图是什么，请直接翻到题目分析 QwQ
- 如果你是很强很强的大佬，请直接翻到下一篇题解 QwQ
最大权闭合子图::概念

什么是 闭合子图 ？
1. 它是一种子图（逃
2. 它还是有向图的子图。。
3. 它还可以一路走到底，不撞南墙不回头。。。
具体来说，就是：对于每个点，从它出发，能够走到的所有点都属于闭合子图中

举个栗子，对于下面这张图， $\{b, c, d\}$ 、 $\{b, d\}$ 都是它的闭合子图。但是 $\{a, b, d\}$ 却不是，因为从 a 可以走到 c ， c 却不在 $\{a, b, d\}$ 中。

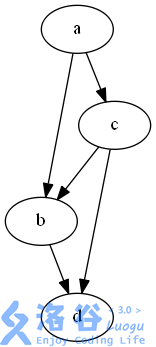
$\text{形式化地（如果你想看的话），若} G'(V', E') \text{是} G(V, E) \text{的一个闭合子图，那么：}$
$V' \in V, E' \in E$
$\forall (u, v) \in E, \text{都有} u \in V' \text{ 且 } v \in V'$
最大权闭合子图就是原图中点权和最大的闭合子图。

这个模型有什么用呢？待我慢慢道来。

最大权闭合子图::实现

最大权闭合子图问题可以使用最小割解决OVO！。

连边方式
- 对于所有原图中的边 $(u, v)$ ，连边 $u \rightarrow v$ ，容量为 $INF$ 。
- 对于每个原图中的点 $u$ ，设 $u$ 的权值为 $val[u]$ ：
  
  若 $val[u] > 0$ （正权点），连边 $S \rightarrow u$ ，容量为 $val[u]$ 。
  
  若 $val[u] < 0$ （负权点），连边 $u \rightarrow T$ ，容量为 $-val[u]$ 。
至于 $val[u] = 0$ （零权点）的情况，向 $S$ 还是 $T$ 连边对答案并没有影响（见下解释），所以可以不做特判。

如图所示，右边是原图，网络流连边如左图所示。

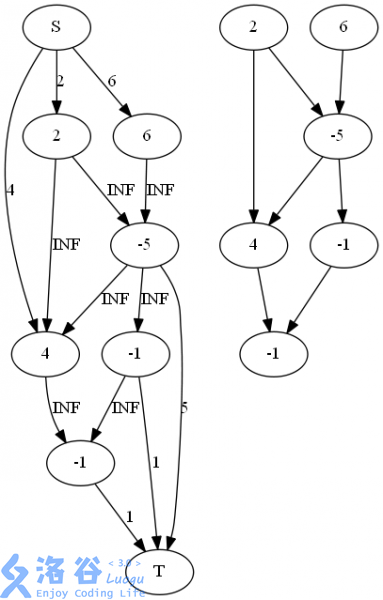
直接在图上跑最小割即可，最大权 = 正点权和 - 最小割，而最大权闭合子图的节点就是与 $S$ 联通的部分。

为什么这样建模是正确的呢？让我们分析一下：

首先，所有不连向 $S$ 或 $T$ 的边容量都是 $INF$ ，不可能被割掉。

这样，能被割掉的边只有连向 $S$ 或 $T$ 的边（这样的割被称为 简单割 ）。

设与 $S$ 联通的节点集为 $X$ ，与 $T$ 联通的节点集为 $Y$ ，那么最大权闭合子图的节点就是 $X$ 集。

一开始假设所有正权点都在（最大权）闭合子图中，

对于某一个正权点 $u$ ，如果割掉它与 $S$ 的连边，意味着将它分到 $Y$ 集合中，不选它作为闭合子图的节点，故闭合子图权值应减去 $val[u]$ 。

对于某一个负权点 $u$ ，如果割掉它与 $T$ 的连边，意味着将它分到 $X$ 集合中，那么闭合子图权值应加上 $val[u]$ ，即减去 $-val[u]$ 。

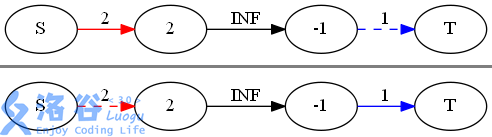
如下图所示，假设这是网络图中的一条路径：

这个图有两种割法，其中割掉蓝色的边花费最小，需要付出 1 的费用。

故这个图中闭合子图的最大权值是 $2 - 1 = 1$ 。

这题跟 最大权闭合子图 有什么关系呢？想必大家已经能够发现一些规律了！

题目分析

规律：

我们看一下题目描述：
```
对于第r行的进攻，Zombies必须首先攻击Pr, M-1；若需要对Pr, c（0≤c<M-1）攻击，必须将Pr,M-1, Pr, M-2 … Pr, c+1先击溃，并移动到位置(r, c)才可进行攻击。
```
```
即便Zombie进入了一个Plant所在的位置，但该位置属于其他植物的攻击位置集合，则Zombie会被瞬间消灭而所在位置的植物则安然无恙
```
题目描述暗示着： 如果你要攻击植物 $i$ ，那么你就必须把 $i$ 的右边一棵植物、以及保护着它的所有植物都一起攻击掉 。

这与最大权闭合子图中 对于每个点，从它出发，能够走到的所有点都属于闭合子图中 刚好契合。

我们可以这样建图：
1. 植物 $i$ 的点权设为 $val[i]$
2. 所有植物 $i$ 向它的右边连边
3. 如果一个植物 $j$ 保护着 $i$ ， $i$ 向 $j$ 连边
在这个图上求出最大权闭合子图，答案就是最大收益，也就是问题的答案。

一个问题

等等，如果你直接写出代码，你会发现你只能拿到可怜的分数（甚至连样例都过不了）

我们漏了一种情况，如果两棵植物互相保护（环），那么僵尸无论如何都无法攻击到它们。

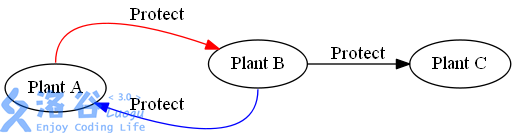
（上面这个图展示的是节点之间的保护关系，事实上在网络图中，边刚好相反）

同理，被环所保护的节点也无法被攻击到。

所有出现在环中以及被环保护的节点都应该被去除。我们可以先建一个反向图（这里是指相对于网络图的反向图），并进行拓扑排序，能够被拓扑排序遍历到的节点才能用来建图。

讲到这里，问题终于解决了！

代码

激动人心的代码时刻！（假的，写得超丑 2333 ）
```
#include<bits/stdc++.h>
using namespace std;
#define POINT(X, Y)  ((X) * 31 + (Y))
const int MAXN = POINT(30, 30) + 10;
const int INF = 2000000000;
const int MAXM = MAXN * MAXN + 10;
struct Graph {
	struct Node {
		int to, cap;
		int next;
	} node[MAXM * 2];
	int top, head[MAXN];
	Graph() {
		top = 1;
	}
	void add(int u, int v, int cap) {
		top ++;
		node[top].to = v;
		node[top].cap = cap;
		node[top].next = head[u];
		head[u] = top;
		top ++;
		node[top].to = u;
		node[top].cap = 0;
		node[top].next = head[v];
		head[v] = top;
	}
	queue<int> Q;
	int dis[MAXN];
	int s, t;
	bool bfs() {
		memset(dis, -1, sizeof(dis));
		dis[s] = 0;
		Q.push(s);
		while(!Q.empty()) {
			int u = Q.front();
			Q.pop();
			for(int i = head[u]; i; i = node[i].next) {
				int v = node[i].to;
				if(dis[v] == -1 && node[i].cap) {
					dis[v] = dis[u] + 1;
					Q.push(v);
				}
			}
		}
		return dis[t] != -1;
	}
	int dfs(int u, int flow) {
		if(u == t)
			return flow;
		else {
			int ret = flow;
			for(int i = head[u]; i && ret; i = node[i].next) {
				int v = node[i].to;
				if(dis[v] == dis[u] + 1 && node[i].cap) {
					int k = dfs(v, min(ret, node[i].cap));
					node[i].cap -= k;
					node[i ^ 1].cap += k;
					ret -= k;
				}
			}
			if(ret == flow)
				dis[u] = -1;
			return flow - ret;
		}
	}
	int dinic() {
		int ans = 0;
		while(bfs())
			ans += dfs(s, INF);
		return ans;
	}
} G;
int n, m;
int score[MAXN];
vector<int> out[MAXN];
int in[MAXN];
bool vis[MAXN];
queue<int> Q;
void toposort() {
	for(int i = 1; i <= n; i ++) {
		for(int j = 1; j <= m; j ++) {
			if(!in[POINT(i, j)]) {
				Q.push(POINT(i, j));
				vis[POINT(i, j)] = true;
			}
		}
	}
	while(!Q.empty()) {
		int u = Q.front();
		Q.pop();
		for(int i = 0; i < out[u].size(); i ++) {
			int v = out[u][i];
			in[v] --;
			if(!vis[v] && !in[v]) {
				Q.push(v);
				vis[v] = true;
			}
		}
	}
}
int main() {
	cin>>n>>m;
	for(int i = 1; i <= n; i ++) {
		for(int j = 1; j <= m; j ++) {
			int cnt;  //  保护植物的棵数
			cin>>score[POINT(i, j)]>>cnt;
			for(int k = 1; k <= cnt; k ++) {
				int x, y;
				cin>>x>>y;
				//  POINT(i, j) <- POINT(x, y)
				x ++;
				y ++;
				out[POINT(i, j)].push_back(POINT(x, y));
				in[POINT(x, y)] ++;
			}
			if(j < m) {
				out[POINT(i, j + 1)].push_back(POINT(i, j));
				in[POINT(i, j)] ++;
			}
		}
	}
	toposort();
	G.s = MAXN - 1;
	G.t = MAXN - 2;
	int sum = 0;
	for(int i = 1; i <= n; i ++) {
		for(int j = 1; j <= m; j ++) {
			int u = POINT(i, j);
			if(!vis[u])
				continue;
			if(score[u] >= 0) {
				G.add(G.s, u, score[u]);
				sum += score[u];
				// printf("S -> [%d, %d] : %d\n", i, j, score[u]);
			}
			else {
				G.add(u, G.t, -score[u]);
				// printf("[%d, %d] -> T : %d\n", i, j, -score[u]);
			}
			for(int k = 0; k < out[u].size(); k ++) {
				int v = out[u][k];
				if(vis[v]) {
					G.add(v, u, INF);
					// printf("[%d, %d] -> [%d, %d] : INF\n", v / 31, v % 31, i, j);
				}
			}
		}
	}
	cout<<sum - G.dinic()<<endl;
	return 0;
}
```
内容会陆续搬运到博客里......