1 条题解
-
0
自动搬运
来自洛谷,原作者为

Clu3ter
这个人很懒,但他还是留下了点什么搬运于
2025-08-24 21:41:45,当前版本为作者最后更新于2019-07-14 11:37:56,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
这道题是一道DP题。
描述状态表示到达第层之上所用的最短时间。
初始状态即为塔底,根本不需要时间。 那么 边界条件 就很明显了:
接着,题目要求的是到达塔外的时间,而塔有层,所以最终要求的解的就是
然后我们自己搞一组数据:
INPUT:
6 5 2 4 5 3 2OUTPUT:
5我们把这组数据画下来:
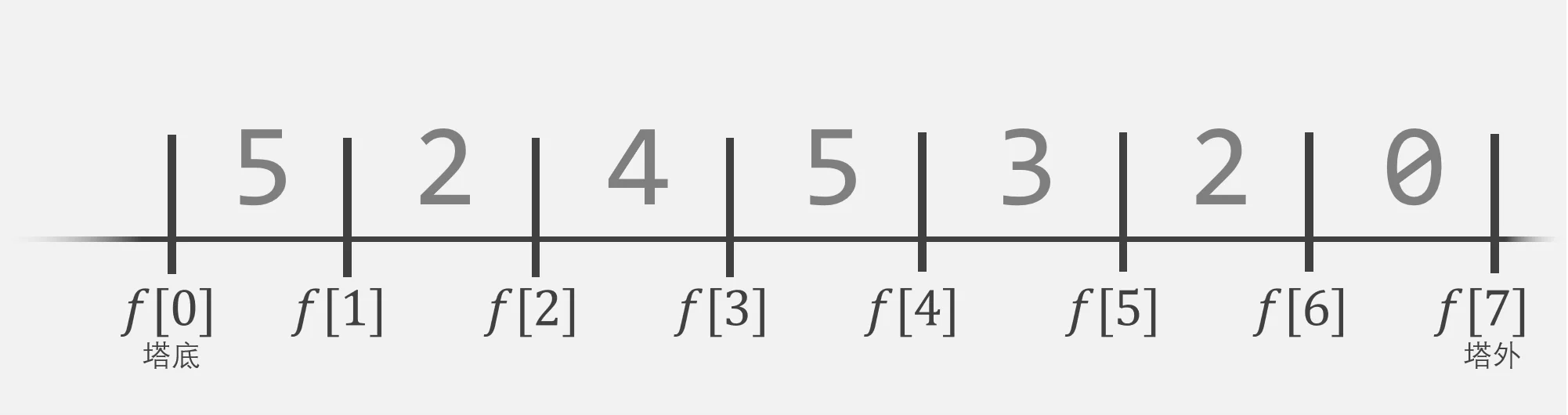 塔底,解是
塔底,解是不难看出,这组数据的走法是:
$$0\Rightarrow 1 \stackrel{2}\rightarrow 2 \Rightarrow 4 \stackrel{3}\rightarrow 5 \Rightarrow 7 $$(表示爬,表示仙术瞬移)
接下来我们来推导
状态转移方程
根据题意,到达第楼有三种方法:
- 徒步爬楼(花费与下层层高相等的时间 )
- 仙术瞬移1层(不花费时间 )
- 仙术瞬移2层(不花费时间 )
也有限制条件:
仙术瞬移无法连续使用
那么也就是说,仙术瞬移之后必须爬楼,
爬楼是世间万物の归宿,是不可避の物,是死亡の灯塔,是宇宙の终结,则爬楼到达第楼的三种方法有所变化:- 从楼徒步爬楼.
( 花费时间 总花费时间 )
- 从楼仙术先瞬移1层到楼,再徒步爬楼.
( 花费时间 总花费时间 )
- 从楼仙术先瞬移2层到楼,再徒步爬楼.
( 花费时间 总花费时间 )
如下图
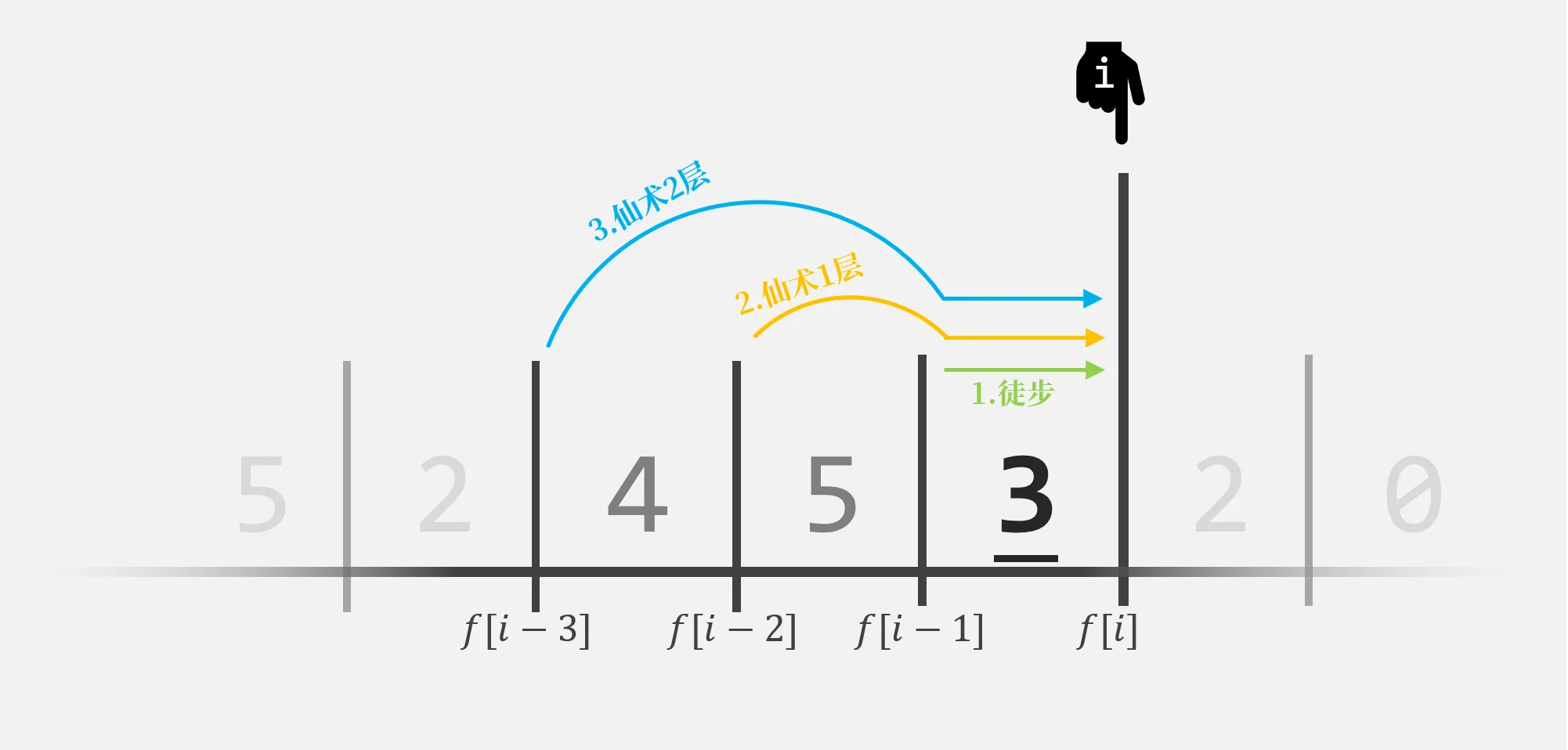
这样的话,就不需要考虑仙术不能连续使用的问题了,
所以,到达第层所需要的最短时间,就是三种方法所需要总时间中的最小值,于是我们成功推导出了状态转移方程:
下面奉上蒟蒻的辣鸡代码,还请垂阅敝码,多多赐教
#include<bits/stdc++.h> using namespace std; int n; int a[1000005]; int f[1000005]; int main() { cin>>n; for(int i=1; i<=n; i++) { cin>>a[i]; f[i]=1e9;//注意初始化 } f[n+1]=1e9; for(int i=1; i<=n+1; i++) {//循环到n+1 f[i]=min(f[i],f[i-1]); f[i]=min(f[i],f[i-2]); f[i]=min(f[i],f[i-3]); f[i]+=a[i]; } cout<<f[n+1];//输出解 return 0;//愉快的结束 }文明查题解,拒绝复制粘贴
『做正确,好懂,好看的题解』
- 1
信息
- ID
- 1863
- 时间
- 1000ms
- 内存
- 125MiB
- 难度
- 2
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者

