自动搬运

查看原文

来自洛谷，原作者为

	学委 希望以后某时候还能来写题！

搬运于2025-08-24 21:41:28，当前版本为作者最后更新于2018-12-28 08:38:38，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

限制条件是——如果要取某一个方格，那么禁止取相邻的四个方格，不限制其它所有方格。

所以猜测，从禁止的角度考虑才会更高效。也就是说，先选中所有方格，再想办法删去权值和尽量小的一批方格。

相邻的概念是，横坐标或纵坐标中的一个相差 $1$，所以两点的横纵坐标之和奇偶性不同。

于是，横纵坐标和的奇偶性相同的两个点肯定不互斥（奇偶性不同的可能互斥）。把互斥的点连边的话，会形成一个二分图。

但先不管这个。

要想办法构造一个模型，它：

• 能删掉一个元素，表示不取这个方格；

• 删掉的代价为方格的权值；

• 要么删掉的总是保证策略最优的，要么能反悔；

• 最终状态为：没有互斥的方格了。

好像能发现对应的模型了，大概是图一类的东西：

• 删掉连向方格的边

• 边权为方格的权值

• 网络流搞一搞

• 割

怎么构造一个合适的图呢？最好能利用上面的二分图。并不容易想到：

源点连向二分图的一个点集（横纵坐标之和为奇数的那些方格），边权为点权。删一条边表示不取这个方格。

二分图的另一个点集连向超级汇，边权还是点权。删边也表示不取此点。

二分图内部的边，连接着互斥的点。边权全部赋为 $inf$，以保证在最小割中不被删。啥意思？

想象一下通过某种方式，求出了该图最小割。

• 因为是最小割，所以中间的 $inf$ 边没删，删掉的都是源点连出的边，或连入汇点的边。

  因此这个割能够确切表示：不取某些方格。（删掉中间边本来就没有意义，不能表示对方格的操作；只有两侧的边具有意义）

• 因为是割，所以图不连通。不连通，就已经保证没有取到任何互斥的方格（假设图中还有互斥方格，也就是两者在图中各自所属的边还没删，再因为它们中间的 $inf$ 边也没删，所以图还是连通的）

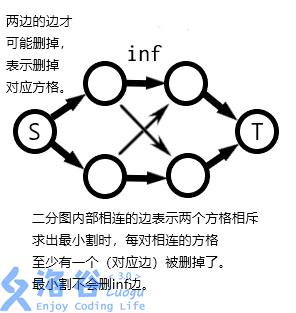
最后只需知道最大流 = 最小割就好了。

//Dinic 理解代价低 
#include <cstdio>
#include <cctype>
#include <cstring>
#include <queue>
#define N 10010
#define E 100010
#define S 0
#define T (m * n + 1)
#define code(i, j) ((i - 1) * m + j)//点的线性标号 
#define between(x, flo, top) (flo <= x and x <= top)//您是不是不喜欢这个qwq 
int getint() {
	int res = 0, ch = getchar();
	while (!isdigit(ch) and ch != EOF)
		ch = getchar();
	while (isdigit(ch))
		res = res * 10 + (ch - '0'), ch = getchar();
	return res;
}
inline int min(int x, int y) { return (x < y) ? x : y; }
using std::queue;
const int d[4][2] = {//待会枚举四个方向用的 
	{0, 1},
	{0, -1},
	{1, 0},
	{-1, 0}
};

int m, n;
int sum = 0;

int first[N];
int nxt[E], to[E], val[E], cnt = 1;
void addE(int u, int v, int w) {
	++cnt;
	to[cnt] = v;
	val[cnt] = w;
	nxt[cnt] = first[u];
	first[u] = cnt;
}

int dep[N];
queue<int> q;
bool bfs() {
	memset(dep, 0, sizeof(dep));
	
	dep[S] = 1;
	q.push(S);
	while (not q.empty()) {
		int u = q.front();
		q.pop();
		for (int p = first[u]; p; p = nxt[p]) {
			int v = to[p];
			if (dep[v])
				continue;
			if (val[p]) {//放心，开始都是正权的情况下，不会出现负数的 
				dep[v] = dep[u] + 1;
				q.push(v);
			}
		}
	}
	return dep[T];
}

int dfs(int u, int in) {
	if (u == T)
		return in;
	int out = 0;
	for (int p = first[u]; p and in; p = nxt[p]) {
		
		if (val[p] == 0)
			continue;
		int v = to[p];
		if (dep[v] != dep[u] + 1)
			continue;
		
		int res = dfs(v, min(val[p], in));
		val[p] -= res;
		val[p ^ 1] += res;
		in -= res;
		out += res;
	}
	
	return out;
}

int main() {
	n = getint(), m = getint();
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= m; ++j) {
			int w = 0;
			sum += w = getint();//假定全部都取，随后会删 
			if ((i + j) % 2 == 0) {//阵营A，源点连向自己，自己连向阵营B 
				addE(S, code(i, j), w);
				addE(code(i, j), S, 0);
				
				for (int k = 0; k <= 3; ++k) {
					int x = i + d[k][0], y = j + d[k][1];
					if (between(x, 1, n) and between(y, 1, m)) {
						addE(code(i, j), code(x, y), 2e9);
						addE(code(x, y), code(i, j), 0);
					}
				}				
			}
			else {//阵营B，连向汇点 
				addE(code(i, j), T, w);
				addE(T, code(i, j), 0);
			}
		}
	
	int cut = 0;//最小割 
	while (bfs())
		cut += dfs(S, 2e9);//最小割 = 最大流 
	printf("%d\n", sum - cut);
	return 0;
}