自动搬运

查看原文

来自洛谷，原作者为

	lukelin 抱歉，我已经不能再获得更多的幸福了...

搬运于2025-08-24 21:40:19，当前版本为作者最后更新于2019-07-09 16:01:44，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

前言

更好的阅读体验:
   我的博客

题解

这道题目我是按表格中的列来考虑的，

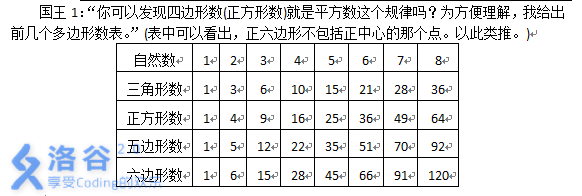
设读入的数字为$x$，考虑上面的表格。
我们发现如果当前为第$k$列，那么该列每行之间都差了$1+2+\dots+(k-1)$。
于是我们暴力枚举列号，如果当前的$x$满足$(x-k)\ \%\ (1+2+\dots+(k-1))=0$的话,
显然$x$是珂以成为一个多边形数的。
设它为$n$边形，那么显然$n=(x-k)\ /\ (1+2+\dots+(k-1))+2$
然后我们发现每一个边形数的第一个都是它自己，因此除了$2$以外不会有$poor$,特判一下即可。
还有一个$1$也需要特殊处理，它应该输出$3$和$4$。

代码

#include <cstdio> 

int read(){
    int x = 0; int zf = 1; char ch = ' ';
    while (ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
    if (ch == '-') zf = -1, ch = getchar();
    while (ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar(); return x * zf;
}

int main(){
    int ng = read();
    while (ng--){
        int x = read(), ans1 = 0, ans2 = 0;
        if (x == 1){puts("3 4"); continue;}
        else if (x == 2){puts("Poor2"); continue;}
        /*n边形数  k + (n - 2) * (1 + 2 + ... + k)*/
        long long sum = 1;
        for (int k = 2; ; ++k){
            if (sum + k > x) break;
            int lft = x - k;
            if (!(lft % sum)){
                int ans = lft / sum + 2;
                if (ans >= 3){
                    if (ans < ans1 || (!ans1))
                        ans2 = ans1, ans1 = ans;
                    else if (ans < ans2 || (!ans2))
                        ans2 = ans;
                }
            }
            sum += k; 
        }
        if (ans1) printf("%d", ans1);
        if (ans2) printf(" %d\n", ans2);
        else puts("");
    }
    return 0;
}