自动搬运

查看原文

来自洛谷，原作者为

	b6e0_ ‪

搬运于2025-08-24 21:40:11，当前版本为作者最后更新于2021-07-12 23:26:33，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目链接：https://www.luogu.com.cn/problem/P2664

有几篇 $\mathcal O(n)$ 解法的题解，但是都写的过于不清晰，甚至我会了还是看不懂，于是我重新从头到尾讲一遍 $\mathcal O(n)$ 的算法，尽量包含到每个细节。虽然不能完全确定我的和已经在这儿的题解完全一样，但是大致肯定都是一样的。

在本篇题解中，称节点 $i$ 的颜色为 $a_i$，节点 $i$ 的答案为 $sum_i$（如题面中）。

首先对求 $sum_i$ 的问题做出一个转换：对于每种颜色 $c$，计算有多少条从 $i$ 出发的路径不包含这种颜色，记为 $t_{i,c}$（此处看 $t$ 数组是 $n^2$ 的，这个疑问下面再解决）。那么 $n-t_{i,c}$ 就是有多少条从 $i$ 出发的路径包含颜色 $c$。这段的总体思想就是考虑每种颜色的贡献，再反过来算。

对于一种颜色 $c$，如果将所有颜色为 $c$ 的节点删除，与它连接的边也删除，那么整棵树会断成一些小的连通块（也就是其他题解中的“小树”）。对于任意一个连通块，它内部任意两个点之间在原树上的路径都不会有颜色 $c$。相反地，对于两个点，如果它们在不同的连通块内，那么它们之间在原树上的路径中一定有颜色 $c$。所以，对于一个大小为 $s$ 的连通块中的所有点 $x$，需要把 $t_{x,c}$ 加上 $s$。

如果第一重循环枚举了一个颜色，那么不管怎样都要遍历整棵树（即使有不遍历的方法也会非常复杂，大概这么觉得吧），时间复杂度就变为了 $\mathcal O(n^2)$，不能接受。于是，我们需要在一遍 dfs 中同时处理多种颜色，计算多种颜色的答案。

设当前枚举到了节点 $x$，它有若干子节点 $y_1,y_2,\cdots$。可以发现，如果我们删除掉所有颜色为 $a_x$ 的节点，那么一定存在一些连通块的“顶部”是 $y_1,y_2,\cdots$。下面的图表示了一个子节点 $y$ 的情况。红色圈起来的部分是一个以 $y$ 为顶部的连通块，它的大小是 $y$ 的子树大小减去 $y$ 的子树中所有颜色为 $c$ 的子树的大小。也就是说，我们在一个节点只处理一个颜色，即当前节点的颜色，也只需要处理这个颜色。如果没懂的话见代码实现难点的部分。

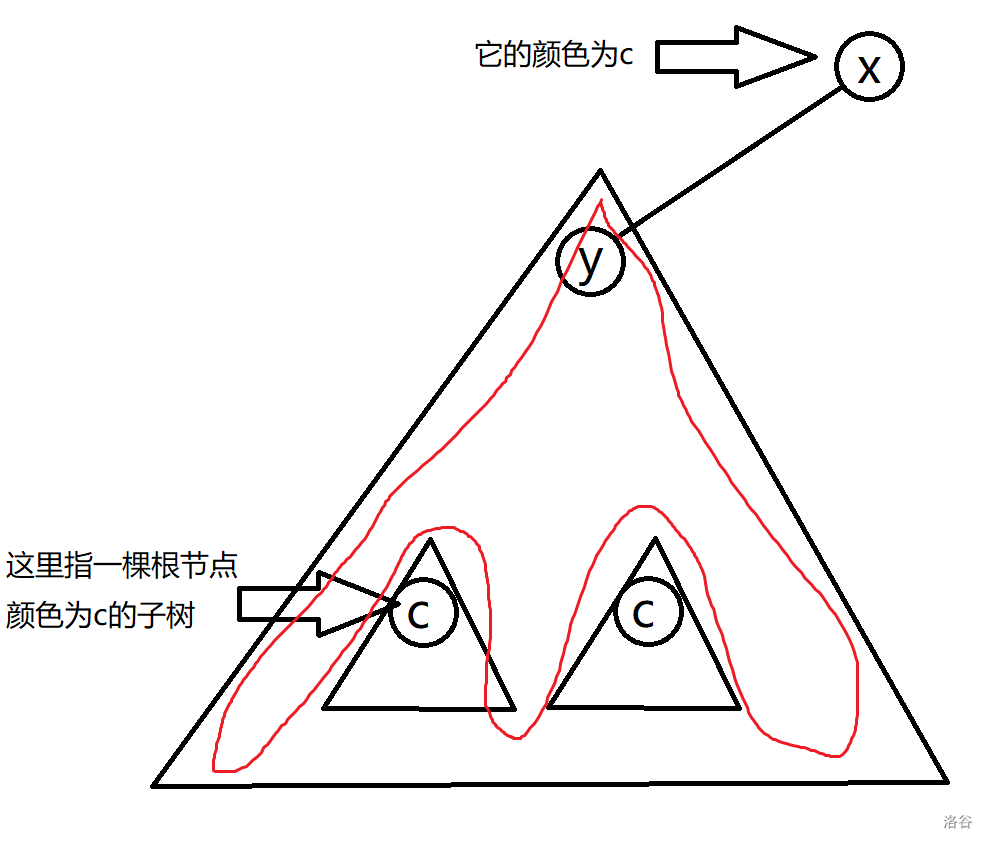
于是，我们能在一遍 dfs 中知道需要给 $t$ 数组的哪些位置加上什么数。下面要解决的就是优化掉 $t$ 的一维并且快速做加法。

在最后，$sum_i$ 是（$m$ 为颜色种数）：

于是我们只需要对于一个 $i$，求出所有颜色的答案的和就行了。记为 $t_i$。下面采用树上差分：设我们 dfs 到了 $x$，枚举到了子节点 $y$（也就是这个连通块的顶是 $y$），连通块的大小为 $s$，那么在节点 $y$ 处加 $s$，子树内最靠上的颜色为 $c$ 的节点处减 $c$。你肯定没看懂，看下图（如何求答案、正确性、复杂度证明等在图下）：

最后 $t_x$ 是从 $x$ 到根节点路径上的差分值的和。这样，上图中那些 $c$ 的子树内就不会受到这个连通块带来的贡献（抵消了），$x$ 及外面更不会受到贡献（$x$ 确实不应该受到贡献）。

有关这个解法的复杂度，看起来一个一个给 $y$ 子树内的 $c$ 打标记很慢，其实，在一个节点以“$c$”的身份被打过标记后就再也不会以“$c$”的身份被打标记了。以“$y$”的身份打标记也显然只会有一次，所以总复杂度是 $\mathcal O(n)$ 的。至此，这个问题被完美解决。

代码实现还有几个不太好处理的细节：

• 如何快速计算 $y$ 的子树内那些如图中 $c$ 的子树大小的和，也就是连通块相比 $y$ 的子树缺失的部分。为解决这个问题，我们以颜色为下标开一个桶 $b_x$（即代码中的 colsiz[x]）记录那些极大的、根节点的颜色为 $x$ 的子树大小和。在 dfs 到 $x$，准备递归进入它的一个儿子 $y$ 前记录下 $b_{a_x}$ 的值（代码中的 psiz），在回来时比较一下现在的 $b_{a_x}$ 与之前的 $b_{a_x}$，差就是连通块相比 $y$ 的子树缺失的部分的大小。
• 对于上面的 $b$（colsiz）数组的更新，在每一个儿子 $y$ 算出连通块的大小 $s$（代码中的 nsiz）时，都将 $b_{a_x}$ 加上 $s$。最后在枚举完儿子后再加 $1$（节点 $x$）。
• 在打差分标记时，如何找出 $y$ 子树内如图中的那些 $c$ 节点打上减的标记。对于每种颜色 $c$ 开一个 vector（代码中的 v[c]），记录下所有（不管是否在 $y$ 的子树）根节点颜色为 $c$ 且极大的子树的根节点。在需要打标记时，由于刚刚递归进 $y$ 的子树，所以 $y$ 的子树内那些需要打标记的节点肯定在 $v_{a_x}$ 中的最前面。从 $v_{a_x}$ 的后面往前面循环，使用 dfs 序判断是否在 $y$ 的子树内，每找到一个符合要求的就打上标记并由于它不再极大了，执行 pop_back。在循环完所有子节点后，将 $x$ 压进 $v_{a_x}$ 中即可。
• 在第一遍 dfs 执行完后，对于每种颜色还剩下根节点那儿的一个连通块。利用当前记录下的 colsiz[c]，v[c] 等信息在主函数内打标记即可，具体见代码。

完整代码：

#include<bits/stdc++.h>
using namespace std;
struct edge
{
	int to,nxt;
}e[200005];
int h[100005],a[100005],dfn[100005],siz[100005],colsiz[100005],cnt;
long long cf[100005],dep[100005];
bool buc[100005];
vector<int>v[100005];
inline int read()
{
	char c=getchar();
	int x=0;
	while(c<'0'||c>'9')
		c=getchar();
	while(c>='0'&&c<='9')
	{
		x=(x<<3)+(x<<1)+c-'0';
		c=getchar();
	}
	return x;
}
void write(long long x)
{
	if(x>9)
		write(x/10);
	putchar(x%10+'0');
}
inline void adde(int x,int y)
{
	e[++cnt].to=y;
	e[cnt].nxt=h[x];
	h[x]=cnt;
}
void dfs(int x,int f)
{
	siz[x]=1;
	dfn[x]=++cnt;
	for(int i=h[x];i;i=e[i].nxt)
		if(e[i].to!=f)
		{
			int psiz=colsiz[a[x]];//记录下递归前的个数
			dfs(e[i].to,x);
			siz[x]+=siz[e[i].to];
			int nsiz=siz[e[i].to]+psiz-colsiz[a[x]];//此处意为siz[e[i].to]-(colsiz[a[x]]-psiz)
			colsiz[a[x]]+=nsiz;
			cf[e[i].to]+=nsiz;//打上加的标记
			while(v[a[x]].size()&&dfn[v[a[x]].back()]>dfn[x])//从后往前找
			{
				cf[v[a[x]].back()]-=nsiz;
				v[a[x]].pop_back();
			}
		}
	colsiz[a[x]]++;
	v[a[x]].push_back(x);
}
void dfs2(int x,int f)//根据差分数组计算最终答案
{
	dep[x]=dep[f]+cf[x];
	for(int i=h[x];i;i=e[i].nxt)
		if(e[i].to!=f)
			dfs2(e[i].to,x);
}
int main()
{
	int n=read(),m=0,tot=0,i,x,y;
	for(i=1;i<=n;i++)
	{
		a[i]=read();
		m=max(m,a[i]);
		buc[a[i]]=true;//记录一个颜色是否出现在a[i]中
	}
	for(i=1;i<n;i++)
	{
		x=read();
		y=read();
		adde(x,y);
		adde(y,x);
	}
	cnt=0;
	dfs(1,0);
	for(i=1;i<=m;i++)//处理包含1的那些连通块
		if(buc[i])
		{
			tot++;
			cf[1]+=n-colsiz[i];
			for(int j=0;j<v[i].size();j++)
				cf[v[i][j]]-=n-colsiz[i];
		}
	dfs2(1,0);
	for(i=1;i<=n;i++)
	{
		write(1ll*n*tot-dep[i]);
		putchar('\n');
	}
	return 0;
}