自动搬运

查看原文

来自洛谷，原作者为

	kradcigam 永不放弃之心，将成为贯穿逆境之光！

搬运于2025-08-24 21:39:58，当前版本为作者最后更新于2019-08-28 15:32:45，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

前言

其实这道题的关键就是在于预处理，其方法类似于 合唱队形

正文

求最大子段和

要想求出双子序列最大和，首先我们要会求出最大子段和

最大子段和的求值方法很简单

定义 $f_i$ 为以第 $i$ 个数结尾的最大子段和

#include <bits/stdc++.h>
using namespace std;
int f[1000010],a[1000010];
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i];
    f[1]=a[1];
	for(int i=2;i<=n;i++)f[i]=max(f[i-1]+a[i],a[i]);
	int ans=f[1];
	for(int i=2;i<=n;i++)ans=max(ans,f[i]);
	cout<<ans;
	return 0;
}

求双子序列最大和

那么我们现在可以去求双子序列最大和

怎么求，思路是 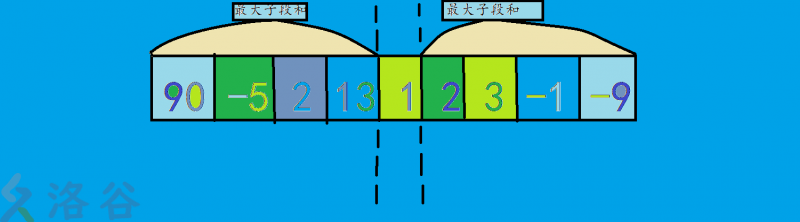如果你去枚举中间的数，然后去算左边的最大子段，再算出右边的最大子段，加起来，用打擂法，求出最大值，你会 $TLE$，毕竟$n<=10^{6}$

那怎么办？我们可以预处理

我们可以用 $O(n)$ 的时间计算到前 $i$ 个数的最大子段，

我们可以用 $O(n)$ 的时间计算到后 $i$ 个数的最大子段

像这样

cin>>n;
for(int i=1;i<=n;i++)cin>>x[i];
f[1]=x[1];
for(int i=2;i<=n;i++)f[i]=max(f[i-1]+x[i],x[i]);//算最大子段
for(int i=2;i<=n;i++)f[i]=max(f[i-1],f[i]);//更新成最大值
l[n]=x[n];
for(int i=n-1;i>=1;i--)l[i]=max(l[i+1]+x[i],x[i]);//算最大子段
for(int i=n-1;i>=1;i--)l[i]=max(l[i+1],l[i]);//更新成最大值

这里 $f_i$ 表示前 $i$ 个数中的最大字段和

这里 $l_i$ 表示后 $i$ 个数中的最大字段和

然后，用 $O(n)$ 的时间去枚举中间的数，打擂法求出双子序列最大和

上代码：

#include<bits/stdc++.h>
using namespace std;
long long x[1000010],f[1000010],l[1000010];
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)cin>>x[i];
    f[1]=x[1];
    for(int i=2;i<=n;i++)f[i]=max(f[i-1]+x[i],x[i]);//算最大子段
	for(int i=2;i<=n;i++)f[i]=max(f[i-1],f[i]);//算最大子段
	l[n]=x[n];
    for(int i=n-1;i>=1;i--)l[i]=max(l[i+1]+x[i],x[i]);//算最大子段
	for(int i=n-1;i>=1;i--)l[i]=max(l[i+1],l[i]);//算最大子段
	long long ans=f[1]+l[3];
	for(int i=3;i<n;i++)ans=max(ans,f[i-1]+l[i+1]);//枚举中间数
	cout<<ans;
	return 0;
}

后记

这种预处理的方法可以优化我们的时间复杂度，避免重复计算，使我们的程序跑得更快！

感谢 @kuoluo03 帮我指出错误，已改正。