自动搬运

查看原文

来自洛谷，原作者为

	流水行船CCD 果 果 没 有 特 权 ~

搬运于2025-08-24 21:39:38，当前版本为作者最后更新于2024-01-02 21:52:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

其他题解的思路都有点看不懂，而且很多图片崩了，来发一发蒟蒻认为比较清晰的思路。

Part1 基本框架

• 求至少有一个点的矩形很麻烦，但是求一个点都没有的矩形就比较清晰，考虑正难则反，最后用总矩形数做差即可得到答案。

• 直接算矩形不好算，这里定一求一，因此枚举矩形下边界，快速计算合法矩形个数，让后就变成了如图问题。

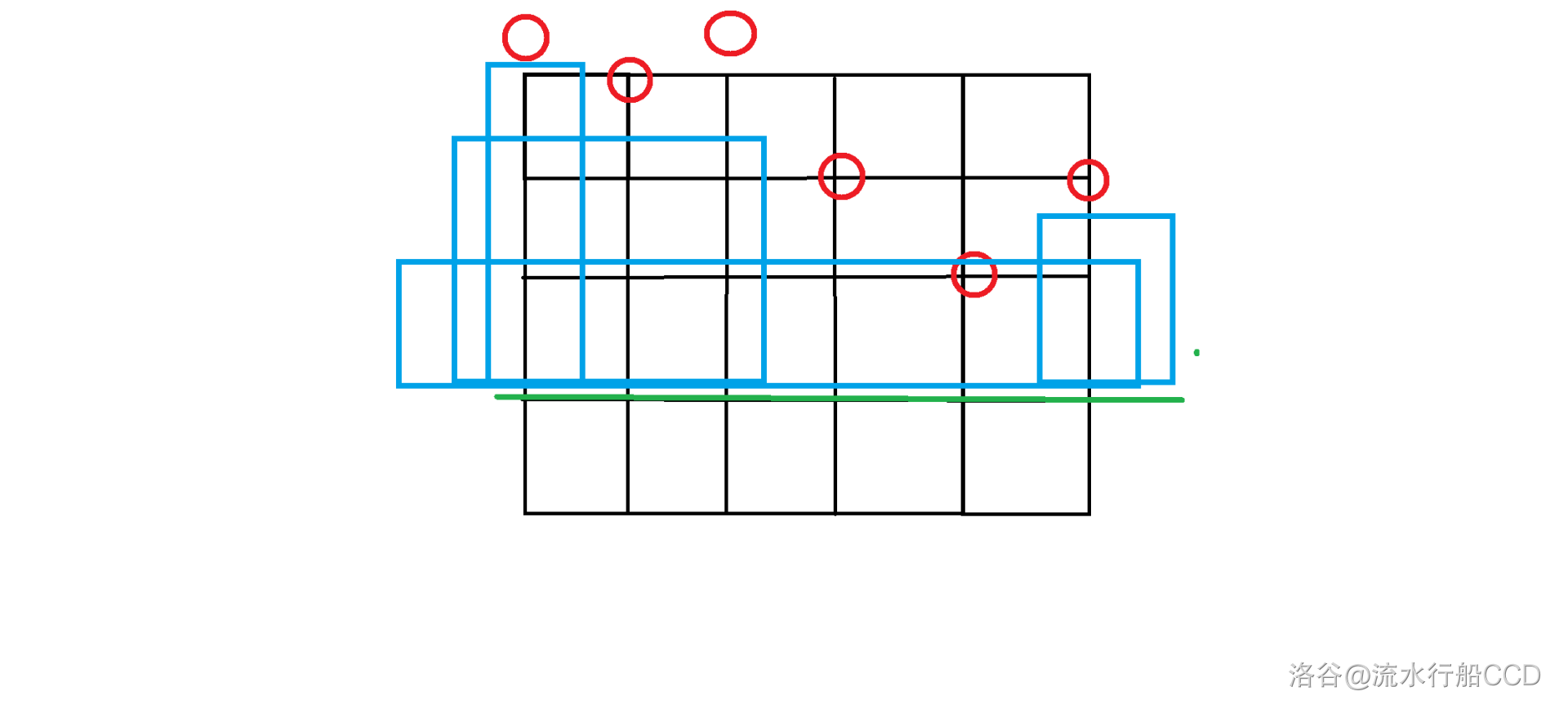
没有资源点的列可以看作在第 $0$ 行有一个资源点，同一列有多个资源点的可以看作仅有最下方的哪一个点。

• 可以看到，如果将这些二维点连起来，可以得到一颗笛卡尔树，而矩形计数问题，就可以转换为经典问题树上计数，即计算每个点下方没有任何资源点，且下边界在枚举位置的矩形个数。

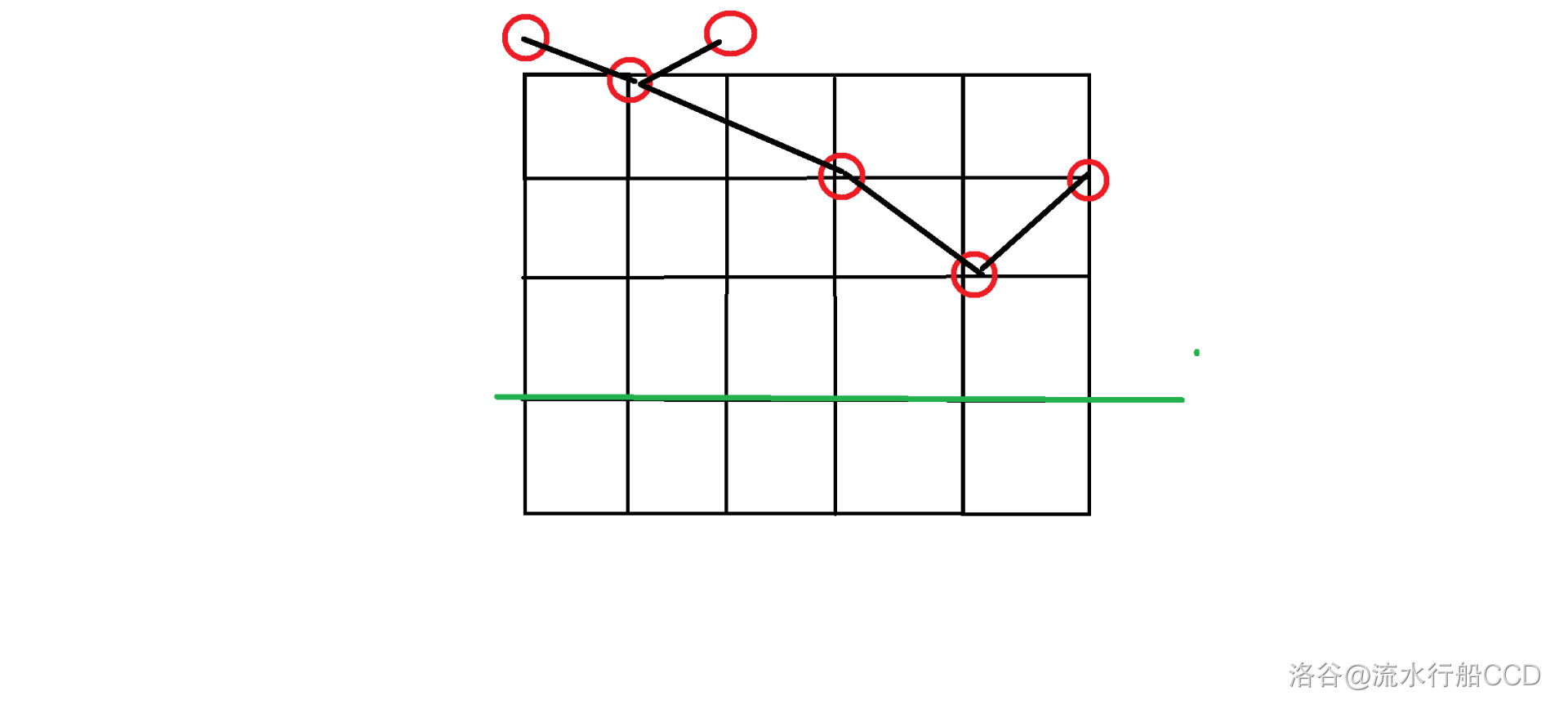
• 由于从上往下建树会导致修改下边界时需要更新每一个点的答案，考虑从下往上进行建树，即根在最下方的那个点。然后对于一个点，其儿子贡献的矩形个数为，这里以右儿子为例，左儿子同理，具体可以结合图片绿色方框理解。

$$\Delta Ans=C^{2}_{sz_{ls}} \times (high_x - high_ls) $$

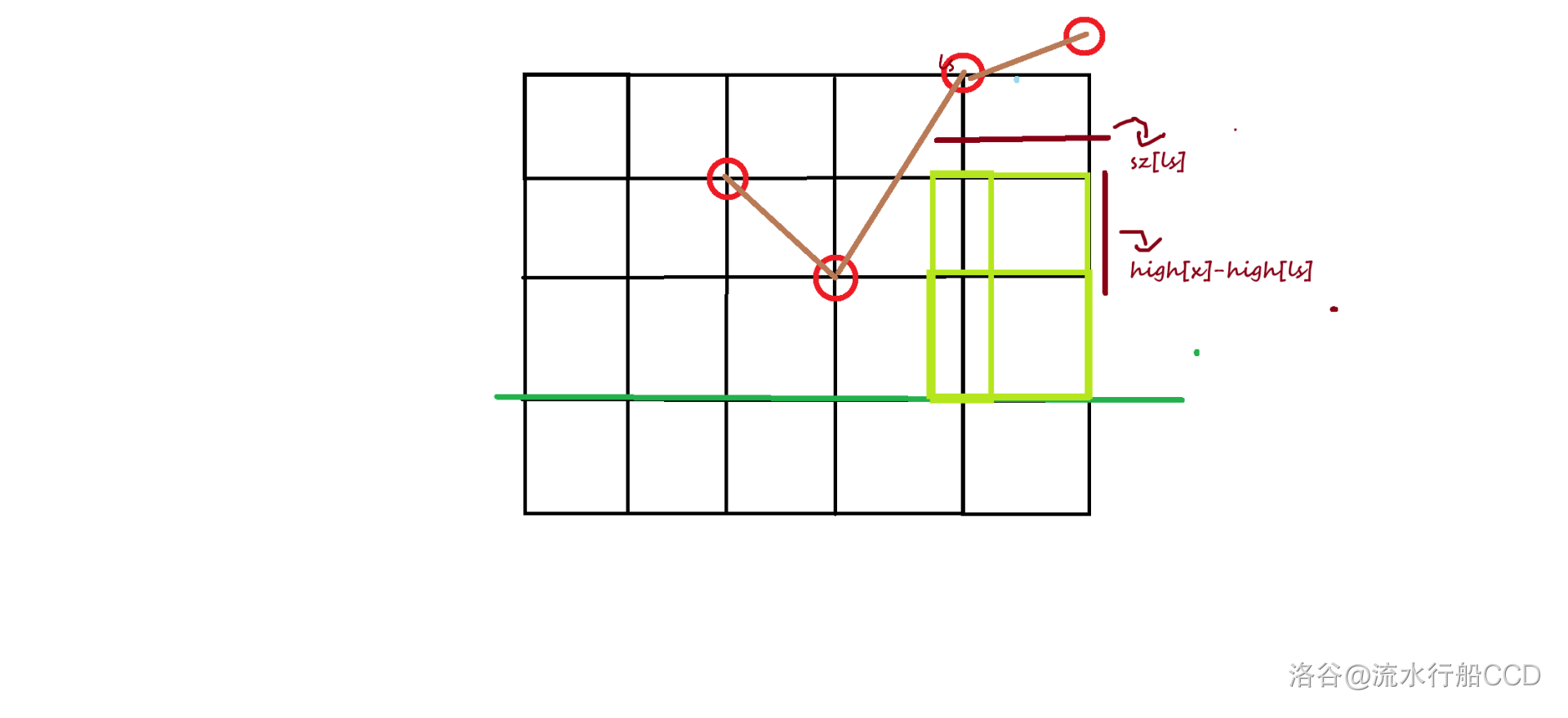
• 而后，由于朴素笛卡尔树不支持删除，所以对于每一个横坐标，重新建笛卡尔树求解，注意根到当前扫描下边界的矩形个数需要单独计算，复杂度 $O(R \times C)$，无法通过。

优化

考虑优化，瓶颈在于删除操作，想到 fhq-Treap 也是一种笛卡尔树，且支持删除，考虑把原本随机赋值的堆性质变量换成每一个点的横坐标，即可动态维护，使用 pushup 统计答案。

由于题目保证点随机，期望 $O(R \log_2 C)$，可以通过。

AC Code

小技巧：可以在初始化时把没有资源点看作是在第零行有一个资源点，这样会避免讨论边界。

#include<bits/stdc++.h>

#define ll long long
#define int long long
#define ull unsigned long long
#define mp make_pair
#define pb emplace_back
#define sort stable_sort
#define REP(i,l,r) for(int i=l;i<=r;++i)
#define PER(i,r,l) for(int i=r;i>=l;--i)
 
using namespace std;
 
const int inf=1e9+7;
const ll INF=1e18+7;
 
random_device R;
mt19937 G(R());
inline int rd(int l,int r){return uniform_int_distribution<int>(l,r)(G);}
 
char buf[1<<19],*p1=buf,*p2=buf;
#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<19,stdin),p1==p2)?EOF:*p1++)
static inline int read() {
	register int x=0;
	register char ch=gc();
	while(ch<'0'||ch>'9') ch=gc();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gc();
	return x;
}
 
 //奇怪的缺省源
 
namespace Code{
	const int N=1e5+7;
	int R,C,n;	
	struct dot{int x,y;}wiki[N];
	inline bool cmp(dot a,dot b){return a.x==b.x?a.y<b.y:a.x<b.x;}
	struct box{
		int son[2];
		int pri,val,sz;
		int ans;
	}tr[N];
	int rt;
#define ls tr[x].son[0]
#define rs tr[x].son[1]
	inline int js(int r,int c){return r*((c*(c+1))>>1ll);}
	inline void pu(int x){
		tr[x].sz=1+tr[ls].sz+tr[rs].sz;
		tr[x].ans= tr[ls].ans+js(tr[x].pri-tr[ls].pri,tr[ls].sz);
		tr[x].ans+=tr[rs].ans+js(tr[x].pri-tr[rs].pri,tr[rs].sz);
		// if(x==2){cout<<tr[rs].sz<<"DEBUG\n";}
	}
	int build(int l,int r){
		if(l>r)return 0;
		int mid=(l+r)>>1;
		tr[mid].son[0]=build(l,mid-1);
		tr[mid].son[1]=build(mid+1,r);
		pu(mid);return mid;
	}
	void split(int x,int &l,int &r,int key){
		if(!x){l=r=0;return;}
		if(tr[x].val<=key)l=x,split(rs,tr[l].son[1],r,key),pu(l);
		else              r=x,split(ls,l,tr[r].son[0],key),pu(r);
	}
	void merge(int &x,int l,int r){
		if(!l||!r){x=l|r;return;}
		if(tr[l].pri>tr[r].pri)x=l,merge(rs,tr[l].son[1],r),pu(x);
		else                   x=r,merge(ls,l,tr[r].son[0]),pu(x);
	}
	void change(dot node){
		int l,tmp,r;
		split(rt,l,r,node.y),split(l,l,tmp,node.y-1);
		tr[tmp].pri=node.x;
		// cout<<node.y<<'C'<<node.x<<'\n';
		merge(l,l,tmp),merge(rt,l,r);
	}	
	// void Print()
	signed main(){
		R=read(),C=read(),n=read();
		REP(i,1,n)wiki[i].x=read(),wiki[i].y=read();
		sort(wiki+1,wiki+n+1,cmp);
		REP(i,1,C)tr[i].val=i,tr[i].pri=0,tr[i].sz=1,tr[i].ans=0;
		rt=build(1,C);
		register int tot=0,Ans=0;
		REP(i,1,R){
			while(tot<n&&wiki[tot+1].x==i)change(wiki[tot+1]),++tot;
			Ans+=tr[rt].ans+js(i-tr[rt].pri,tr[rt].sz);
			// cout<<i<<":"<<rt<<' '<<tr[rt].ans<<' '<<js(i-tr[rt].pri,tr[rt].sz)<<'\n';
			// int x=rt;
			// cout<<"mmp:"<<tr[ls].sz<<' '<<tr[rs].sz<<' '<<js(tr[x].pri-tr[rs].pri,tr[rs].sz)<<'\n';
		}
		cout<<((R*(R+1)>>1ll)*(C*(C+1)>>1ll))-Ans<<'\n';
		return 0;
	}
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	Code::main();
	return 0;
}