自动搬运

查看原文

来自洛谷，原作者为

	llzzxx712 屑大三

搬运于2025-08-24 21:39:28，当前版本为作者最后更新于2019-12-13 15:58:01，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P2597[灾难]

更好的阅读体验

2020.9.18 Update:修改了代码里的入队一个小 bug

题目简述

• 输入一个有向森林
• 灾难值：在一个节点被删去后以它为根从上到下逐步删去入度为0的点，最终被删去的点的数量即其灾难值
• 你需要输出每个点的灾难值

比如看样例（一个食物网应该是由食物指向捕食者，在存边时要反向存）

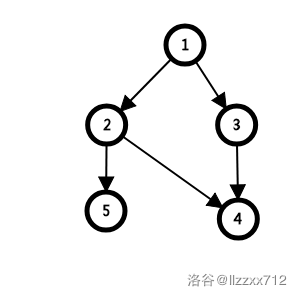
1节点被删去后2、3节点入度变为0被删去，接着4、5节点入度变为0被删去，一共4个点被删去，所以它的灾难值是4.

2被删去会使5节点入度为0被删去，所以它的灾难值为1。剩下几个点被删去都不会产生入度为0的点，他们灾难值为0

题目分析

下面内容来自《中学生计算机程序设计提高篇》（有删减）

对于生产者，不妨给它添加一个假想的食物——太阳。那么这个森林就变成了一颗“灭绝树”。

首先，按照食物网从猎物到捕食者的顺序拓扑排序，有且仅有太阳没有任何入度，所以先将太阳加入灭绝树，之后，依次考虑每个生物 $i$ ,依次考虑构建好排序在 $i$ 之前的生物组成的灭绝树，假设$i$ 的食物有 $p_1,p_2,p_3,\cdots,p_k$(这些节点在拓扑序中比 $i$靠前，$i$ 会灭绝，当且仅当$p_1,p_2,p_3,\cdots,p_k$全部灭绝，当且仅当LCA（$p_1,p_2,p_3,\cdots,p_k$）灭绝。

于是可以在树上加上LCA到$i$ 的边，把$i$ 的边加到树中。处理完后就得到了灭绝树，每个生物的灾难值就是以它为根的子树大小减一

下面是自己的详细理解和对上面的补充

感觉书中说的并不是非常清楚，至少我在设计思路和完成代码时遇到了很多问题（WA了10次的痛）

本题中的LCA和普通LCA有一些差别，1是它是多节点的LCA，再者它是要一边建树一边LCA。而且本题中涉及原树（食物网）和新树（灭绝树），书中没有说在哪里求LCA，如何倍增。

我想到的一种求LCA的方法是：更新迭代LCA

其思路是：给每个数多维护一个值$dad$,用来表示如果此时它要被连入灭绝树中，它应该是哪个点的儿子。一开始将$dad$清为-1，将开始入度为0的点 $p_i$ 的$dad$设为0（太阳）。在拓扑排序取出一个点$i$的时候连接边 $dad[i]->i$ (此时$i$的父亲（根节点的父亲前面已经确定）都已经被处理过了，所以$dad[i]$已经确定（怎么确定的马上会说））。然后更新点$i$相对应的深度和倍增数组（因为$i$的祖先们已经在$i$之前被确定，所以此时的深度和其倍增数组可以唯一确定），接着遍历$i$的儿子们，如果它的儿子$p$的父亲$dad[p]$为0，说明它的父亲还没有被更新过，此时把$dad[p]$更新为$i$。否则就将$dad[p]$更新为LCA（$dad[p],i$）。这样，在遍历到$p$的时候它的父节点就被确定下来了。

为什么能这样做呢？

我们需要在求出在原树上$i$的所有父亲的LCA，就相当于把两个父亲当成一组，一组一组地求LCA，并把这个过程转移到一个点遍历其儿子的时候。

思路总结

1. 初始化$dad$数组为-1。
2. 读入原树，反向建立森林并统计每个点的入度。
3. 扫描所有点，将入度为0的点加入队列中，并将其$dad$更新为0。
4. 拓扑排序，取出队首$x$，连接$dad[x],x$,并更新倍增数组和该点深度。遍历$x$的儿子，更新儿子的$dad$并将儿子的入度减一，若入度为0则入队。
5. 重复操作4，直到队列为空。
6. $dfs$一次新树，并递归求子树大小。
7. 输出每个点子树减一

易错点

• 原树是一个有向无环森林，亲测存边数组大小20w能过
• 倍增数组在根节点再往上是0（如果把太阳设为-1节点就会WA第五个点）
• 存原树时要反向存
• 倍增深度16
• 原树和新树的查询小心弄混
• 输出时子树大小要减一

代码实现

#include<bits/stdc++.h>
#define N 65536
using namespace std;
int n,tot,ans,tot1;
int to[N*4],ne[N*4],head[N];//原树邻接表 
int edge[N],anc[N][21],dad[N],size[N],de[N];// 入度、倍增、父亲、子树大小、深度 
int to1[N*4],ne1[N*4],head1[N];//新树邻接表 
void add(int x,int y) { to[++tot]=y,ne[tot]=head[x],head[x]=tot,edge[y]++; }//存原树 
void add1(int x,int y) { to1[++tot1]=y,ne1[tot1]=head1[x],head1[x]=tot1;}//存新树 
queue < int > q;//STL队列 
void dfs(int x){//深搜求子树大小 
    size[x]=1;
    for(int i=head1[x];i;i=ne1[i]){
        int y=to1[i];
        dfs(y);
        size[x]+=size[y];
    } 
}
int lca(int x,int y){//求LCA 
    if(x==y) return x;
    if(de[x]<de[y]) swap(x,y);
    for(int i=18;i>=0;i--) if(de[anc[x][i]]>=de[y]) x=anc[x][i];
    if(x==y) return x;
    for(int i=18;i>=0;i--) if(anc[x][i]!=anc[y][i]) x=anc[x][i],y=anc[y][i];
    return anc[x][0];
}
void read(int &x) {//快读 
    int f = 1; x = 0;
    char ch = getchar();
    while (ch < '0' || ch > '9')   {if (ch == '-') f = -1; ch = getchar();}
    while (ch >= '0' && ch <= '9') {x = x * 10 + ch - '0'; ch = getchar();}
    x *= f;
}
int main()
{
    read(n);
    for(int i=1;i<N;i++) dad[i]=-1;//初始化 
    for(int i=1;i<=n;i++){
        int x;
        read(x);
        while(x){
            add(x,i);//反向存树 
            read(x);
        }
    }
    for(int i=1;i<=n;i++) 
        if(!edge[i]){
            q.push(i);
            dad[i]=0;//找到入度为0的边 
        }
    while(!q.empty()){
        int x;
        x=q.front();q.pop();//取出队首  
        add1(dad[x],x);
        anc[x][0]=dad[x],de[x]=de[dad[x]]+1;        
        for(int i=1;i<=18;i++) anc[x][i]=anc[anc[x][i-1]][i-1];//更新倍增数组 
        for(int i=head[x];i;i=ne[i]){
            int y=to[i];
            if(dad[y]==-1) dad[y]=x;//父亲之前没有被更新 
            else dad[y]=lca(dad[y],x);//父亲之前已经被更新过 
            if(--edge[y]==0) q.push(y);//入度为0则入队 
        }
    }
    dfs(0);//求子树大小 
    for(int i=1;i<=n;i++)
        printf("%d\n",size[i]-1);//输出 
    return 0;
}
	

写题解不易，给个赞呗