自动搬运

查看原文

来自洛谷，原作者为

	a1a2a3a4a5 蒟蒻可骂，私信互关，互关者备故事来

搬运于2025-08-24 21:39:23，当前版本为作者最后更新于2025-07-06 11:55:04，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

非非非非非非非非非非非非非非非非非非非非非非非非非非非非非非非非非非常好的一道题，我非常喜欢。

考虑如何放一个碗，我们一定要找到一个上面的碗能叠上去，发现 n 非常小，所以可以枚举放入的顺序，模拟一下，考虑如何在前面的碗都确定的情况下找到能卡住的碗，注意到假设我们把当前碗和前面的碗叠中每一个碗都试着卡一下，我们当前碗被 j 碗卡得最靠上，那么肯定是被 j 卡住了。

证明：盗个图

出处：

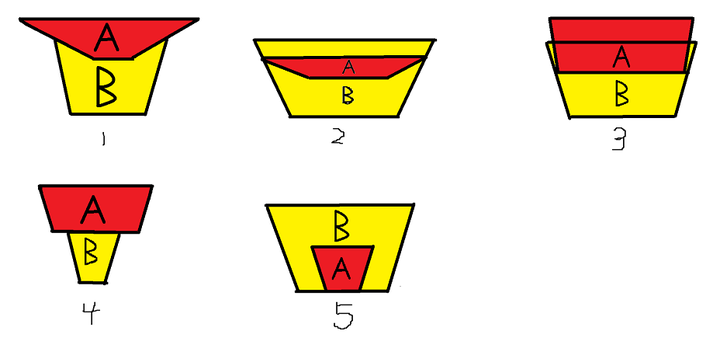
只有在 2 中， B 可能卡住更上面的碗，如果更上的碗刚好被 B 卡住了，那么忽视 B 的边边，假设他被 A 卡住了，高度肯定比 B 卡的低。

枚举排列，枚举被每个碗卡的高度取最大值不断模拟即可。

至于算被卡的高度，我们可以用相似三角形与分类讨论。（注意不是相似梯形，因为他们上底相等，下底不相等，看似相似，实则真的吗？假的！）

具体如何计算，我们用碗边斜率和上碗半径和下碗半径的值来分类讨论上面五个图，题解各神讲的很明白了。

代码：

#include<bits/stdc++.h>
using namespace std;
const int QAQ=11;
int n,p[QAQ];
double da=1e16,h[QAQ],nw[QAQ],o1[QAQ],o2[QAQ];
double xie(int x) {return h[x]/(o2[x]-o1[x]);}
double ju(int a,int b)
{
	if(o1[a]>=o2[b]) return h[b];
	if(o2[a]>o2[b]&&o1[a]<o2[b]&&xie(b)>xie(a)&&(o2[b]-o1[a])/(o2[a]-o1[a])*h[a]<=h[b])
		return h[b]-(o2[b]-o1[a])/(o2[a]-o1[a])*h[a];
	if(o1[a]>o1[b]&&o1[a]<o2[b]&&xie(a)>xie(b)) return h[b]*(o1[a]-o1[b])/(o2[b]-o1[b]);
	if(o2[a]<o2[b]&&o2[a]>o1[b]&&xie(a)<xie(b)&&(o2[a]-o1[b])/(o2[b]-o1[b])*h[b]-h[a]>=0)
		 return (o2[a]-o1[b])/(o2[b]-o1[b])*h[b]-h[a];
	return 0;
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++) cin>>h[i]>>o1[i]>>o2[i],p[i]=i;
	while(1)
	{
		double ans=h[p[1]];
		for(int i=1;i<=n;i++) nw[i]=0;
		for(int i=2;i<=n;i++)
		{
			for(int j=i-1;j;j--)
			{
				double cab=ju(p[i],p[j]);
				if(cab+nw[j]>nw[i]) nw[i]=cab+nw[j];
			}
			ans=max(ans,nw[i]+h[p[i]]);
		}
		da=min(da,ans);
		if(!next_permutation(p+1,p+n+1)) break;
	}
	printf("%d",(int)(da+0.5));
	return 0;
}