自动搬运

查看原文

来自洛谷，原作者为

	syksykCCC 相信并抓住那些源于热爱，忠于自我的每一个可能性

搬运于2025-08-24 21:38:45，当前版本为作者最后更新于2020-02-02 18:43:07，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

发表一下自己关于这题是 卡特兰数 的观点。

我们用 $C_i$ 表示 $N = i$ 时的答案。

首先，显而易见，$C_0 = C_1 = 1$。

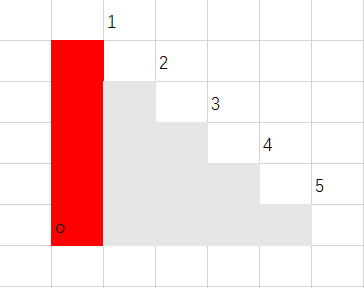
然后呢？我们画一张图:

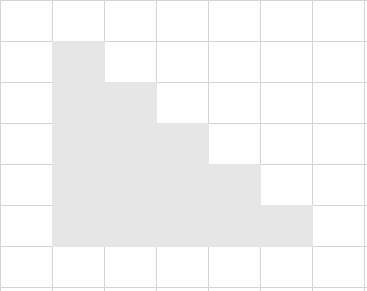
图中所示是 $N = 5$ 的情况。

然后我们看到阶梯的右侧是若干拐角，我们标一下号：

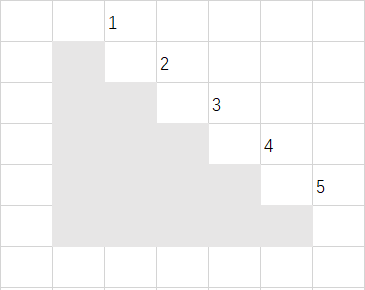
很容易发现，这里有 $N$ 个拐角，而题目只允许我们放 $N$ 个矩形，也就是说，每个矩形恰好覆盖一个拐角。

为啥？如果一个矩形覆盖的拐角 $<1$，那必然有矩形覆盖的拐角 $>1$。那么比如你的矩形覆盖了两个拐角，你不妨画一画那个矩形长成什么样子，自然就明白是不可能的了。

我们把最左下角叫做 $o$ 点，它肯定要被一个矩形覆盖。

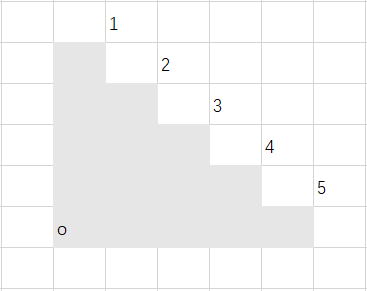
现在，我们枚举一下，覆盖 $o$ 的矩形覆盖了哪一个拐角。

• 覆盖 $1$：

那么右边就是一个 $N = 4$ 的子问题！方案数自然是 $C_4$，但也可以认为是 $C_0 \times C_4$。

• 覆盖 $2$：

上边就是 $N = 1$ 的子问题，右边就是 $N = 3$ 的子问题，根据乘法原理，方案数就是 $C_1 \times C_3$。

• 覆盖 $3$：

上边就是 $N = 2$ 的子问题，右边就是 $N = 2$ 的子问题，根据乘法原理，方案数就是 $C_2 \times C_2$。

• 覆盖 $4$：和覆盖 $2$ 同理。

• 覆盖 $5$：和覆盖 $1$ 同理。

于是，根据加法原理，我们就知道 $C_5 = C_0 \times C_4 + C_1 \times C_3 + C_2 \times C_2 + C_3 \times C_1 + C_4 \times C_0$。

更加的一般一点，我们就发现：

$$C_N = \sum_{i = 0}^{N - 1} C_i \times C_{N - i - 1} $$

这就是卡特拉数了，代码这里就不贴出了，求赞 QwQ。