自动搬运

查看原文

来自洛谷，原作者为

	FlashHu **

搬运于2025-08-24 21:38:33，当前版本为作者最后更新于2018-09-01 22:23:37，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

一进来就看到一个多月前秒了此题的ysn和YCB%%%

最长公共子序列的$O(n^2)$的求解，Dalao们想必都很熟悉了吧！不过蒟蒻突然发现，用网格图貌似可以很轻松地理解这个东东？

设字符串长度为$n,m$，那么想象我们有一个$n+1$行$m+1$列的网格图，只能从左下角往右、上两个方向走。定义每条路径的长度都为$1$。记第$i$行第$j$列为$(i,j)$。

话说网格图真tm难画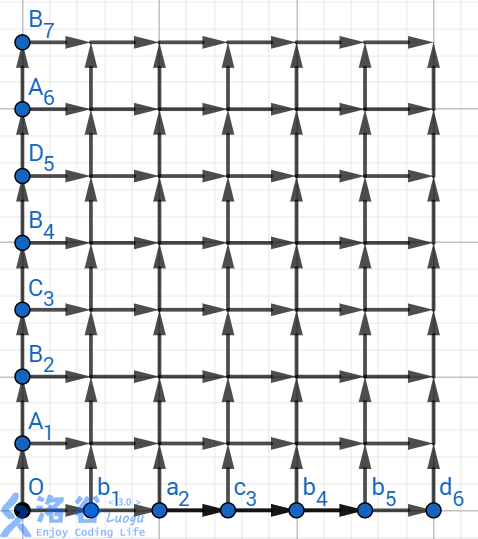

求最长公共子序列本质上是在两个序列中寻找最多的配对，而且这些配对的位置在序列中的位置也要分别递增。

那么，如果$x_i$与$y_j$相等，那么我们就从$(i-1,j-1)$向$(i,j)$连一条边。这在网格图中分明是一条条捷径，那么我们要寻找最长公共子序列，可不可以转化为寻找最短路，或者说寻找经过捷径次数最多的路径呢？

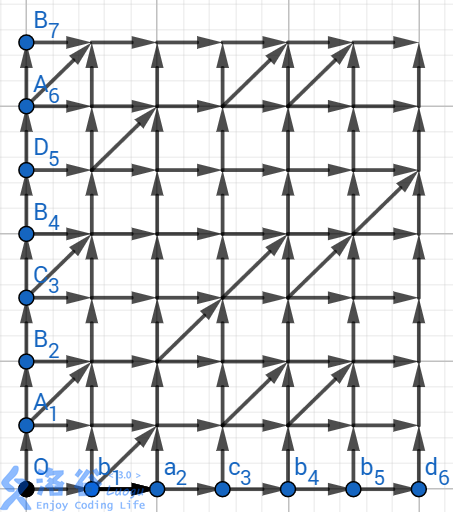
这个模型是很巧妙的，满足了配对的位置在序列中的位置分别递增（因为只能往右、上走）。

那么再看第二问。显然在这个模型中，不同的公共子序列对应的，不是至少有一条边不相同的路径，而是至少有一条捷径不相同的路径。那么这个该怎么DP呢？

设到达$(i,j)$最多能经过的捷径数（即序列的两个前缀的最长公共子序列长度）为$mf_{i,j}$，方案数为$f_{i,j}$。显然$(i,j)$可以从$(i-1,j)$和$(i,j-1)$转移，如果$x_i=y_j$那么还可以从$(i-1,j-1)$转移（$mf$加上$1$）。依次转移，如果新的$mf$更大则直接覆盖原信息，如果$mf$相等则$f$相加。

然而，再次注意不同路径的定义。那么是不是可能存在这样一种情况：到$(i-1,j-1)$的一条路径，分别转移给了$(i-1,j)$和$(i,j-1)$，而再一次转移给了$(i,j)$，没有经过不同的捷径，却计算了两遍！显然只有$mf_{i-1,j-1}=mf_{i,j}$的时候上述情况才会发生，那么这时我们从$f_{i,j}$减去$f_{i-1,j-1}$即可。

思路都清晰了。在开始码DP之前，我们还需要注意这个DP的过程，每行只会从上一行转移，于是使用滚动数组优化空间，防止MLE。

#include<bits/stdc++.h>
#define RG register
#define I inline
#define R RG int
#define G c=getchar()
using namespace std;
typedef long long LL;
const int N=5009,YL=1e8;
char x[N],y[N];
int ff[N],gg[N],mff[N],mgg[N];
int main(){
    scanf("%s%s",x+1,y+1);
    R n=strlen(x+1)-1,m=strlen(y+1)-1,i,j,*f=ff,*g=gg,*mf=mff,*mg=mgg;
    g[0]=1;for(j=0;j<=m;++j)f[j]=1;
    for(i=1;i<=n;++i,swap(f,g),swap(mf,mg)){//滚动数组
        memset(g +1,0,m<<2);//注意清空
        memset(mg+1,0,m<<2);
        for(j=1;j<=m;++j){//三方向转移
            if(x[i]==y[j])mg[j]=mf[j-1]+1,g[j]=f[j-1];
            if(mf[j]>mg[j])mg[j]=mf[j],g[j]=f[j];//覆盖
            else if(mf[j]==mg[j])(g[j]+=f[j])%=YL;//相加
            if(mg[j-1]>mg[j])mg[j]=mg[j-1],g[j]=g[j-1];
            else if(mg[j-1]==mg[j])(g[j]+=g[j-1])%=YL;
            if(mf[j-1]==mg[j])(g[j]+=YL-f[j-1])%=YL;//减掉重复的部分
        }
    }
    printf("%d\n%d\n",mf[m],f[m]);
    return 0;
}