自动搬运

查看原文

来自洛谷，原作者为

	我好蒻呀 **

搬运于2025-08-24 21:38:32，当前版本为作者最后更新于2017-07-15 20:24:03，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

70分算法：费用流

• 我们可以将煤看做流量，通过最小费用最大流来算出我们的最小费用。

• 枚举新厂地址$now$，每次都重新建图，将最大流控制在$\sum{a_i}$，并控制送到两厂的煤的数量，来求最小费用。

• 建图如下：

• 从源点向第$i$座煤矿连一条容量为$a_i$，费用为$0$的边，表示第$i$号矿每年产量为$a_i$吨。

• 从第$i$座煤矿向旧厂连一条容量为$INF$（煤的数量已经在前面限制过），费用为$c_{i,0}$的边，表示从这座煤矿送煤到旧厂的单位费用为$c_{i,0}$（它需要的煤数量会在后面限制，而不能在这里限制，肯定会出错，因为$b$是送到旧厂的煤的总数）。

• 同理，从第$i$座煤矿向新厂连一条容量为$INF$（煤的数量已经在前面限制过），费用为$c_{i,now}$的边，表示从这座煤矿送煤到旧厂的单位费用为$c_{i,now}$。

• 最重要的部分——从原厂向汇点连一条容量为$b$，费用为$0$的边；从新厂向汇点连一条容量为$\sum{a_i}-b$，费用为$0$的边。因为原厂需要$b$个单位的煤矿**（这里要求送来的煤严格等于$b$，不能多也不能少）**，我们需要用这条边限制；对于新厂，因为我们需要将所有煤都送出，因此送到新厂的煤就是$\sum{a_i}-b$，我们也同样连一条边限制。

• 这里我们可以将第$i$座煤矿的编号看做$i$，原厂编号看做$m+1$，新厂编号看做$m+2$，源点汇点编号分别看作$0$和$m+3$。

• 因为旧厂和新厂还有自己的运行费用，而费用流求出来的只是运输费用，因此我们最后还要用(运输费用+$h_0+h_{now}$)来更新答案。

• 建图如下图所示：（cap表示容量，w表示单位费用）

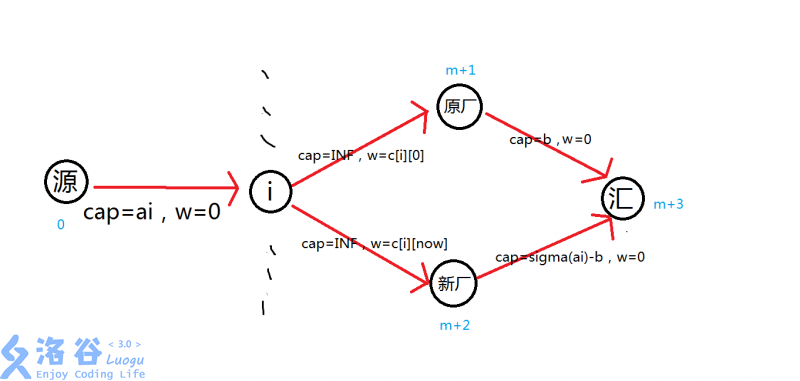
• 代码如下：

#include <cstdio>

inline void read(int &x)
{
    static char ch; 
    while ((ch = getchar()) < '0' || ch > '9'); 
    x = ch - '0'; 
    while ((ch = getchar()) >= '0' && ch <= '9')
        x = (x << 3) + (x << 1) + ch - '0'; 
}

inline int getmin(const int &a, const int &b) {return a < b ? a : b;}

const int MaxN = 55; 
const int MaxM = 5e4 + 10; 
const int MaxB = 1e4 + 10; 
const int INF = 0x3f3f3f3f; 

const int MaxP = MaxM; 
const int MaxE = MaxP * 10; 

int dis[MaxP], src, des; 
int ect = 1, nxt[MaxE], to[MaxE], cap[MaxE], cst[MaxE], adj[MaxP], frm[MaxE], pre[MaxP]; 
int n, m, b, ans = 0, minAns = INF, ansNum; 
int h[MaxN], a[MaxM], c[MaxM][MaxN], tota; 

inline void addEdge(const int &u, const int &v, const int &c, const int &w)
{
    nxt[++ect] = adj[u], adj[u] = ect, to[ect] = v, frm[ect] = u, cap[ect] = c, cst[ect] = w; 
    nxt[++ect] = adj[v], adj[v] = ect, to[ect] = u, frm[ect] = v, cap[ect] = 0, cst[ect] = -w; 
}

inline bool SPFA()
{
    static int q[MaxE << 2], tail; 
    static bool inq[MaxP]; 
    for (int i = src; i <= des; ++i)
        dis[i] = INF; 
    inq[q[tail = 1] = src] = 1; 
    dis[src] = 0; 
    for (int head = 1, u, v, e; inq[u = q[head]] = 0, head <= tail; ++head)
        for (e = adj[u]; v = to[e], e; e = nxt[e])
            if (cap[e] > 0 && dis[v] > dis[u] + cst[e])
            {
                dis[v] = dis[u] + cst[e], pre[v] = e; 
                if (!inq[v])
                    inq[q[++tail] = v] = 1; 
            }
    return dis[des] != INF; 
}

inline void deal()
{
    int minFlow = INF; 
    for (int e = pre[des]; e; e = pre[frm[e]]) minFlow = getmin(minFlow, cap[e]); 
    for (int e = pre[des]; e; e = pre[frm[e]])
    {
        cap[e] -= minFlow; 
        cap[e ^ 1] += minFlow; 
        ans += minFlow * cst[e]; 
    }
}

int now; 
inline void MCMF()
{
    ans = 0; 
    while (SPFA()) deal(); 
    ans += h[0] + h[now]; 
    if (ans < minAns)
        minAns = ans, ansNum = now; 
}

inline void buildGraph()
{
    ect = 1; 
    for (int i = src; i <= des; ++i) adj[i] = 0, pre[i] = 0; 
    src = 0, des = m + 3; 
    for (int i = 1; i <= m; ++i)
        addEdge(src, i, a[i], 0), addEdge(i, m + 1, INF, c[i][0]), addEdge(i, m + 2, INF, c[i][now]); 
    addEdge(m + 1, des, b, 0), addEdge(m + 2, des, tota - b, 0); 
}

int main()
{
    read(m), read(b), read(h[0]), read(n); 
    for (int i = 1; i <= m; ++i) read(a[i]), tota += a[i]; 
    for (int i = 1; i <= n; ++i) read(h[i]); 
    for (int i = 0; i <= n; ++i)
        for (int j = 1; j <= m; ++j)
            read(c[j][i]); 
    for (now = 1; now <= n; ++now)
        buildGraph(), MCMF(); 
    printf("%d\n%d\n", ansNum, minAns); 
    return 0; 
}

100分算法：贪心

• 我们可以枚举新工厂的地址来贪心。

• 设第i个煤矿到新工厂的单位运费为$x_i$，到旧工厂的单位运费为$x_i+delta_i$。

• 那么对于每一单位的煤，它的运费要么是$x_i$，要么是$x_i+delta_i$。

• 由于所有煤的运费中都包含项$x_i$， 有b单位煤的运费中包含项$delta_i$，所以我们只需要使项$delta_i$尽量小，这样就能使整体方案最优。

• 因此我们可以得到以下步骤：

• 枚举新工厂地址$now$；

• 预处理出$delta_i=c[i,0]-c[i,now]$，这里$x_i$就是$c[i,now]$；

• 将煤矿以$delta_i$为关键字从小到大排序。

• 假设我们目前把煤全送到了新工厂，目前费用为$\sum{x_i*a_i}$。那么要有$b$个单位的煤要调到旧工厂，我们贪心将$delta_i$最小的那些煤都送到旧工厂，直到送满$b$为止。每次在第i个煤矿调一单位的煤时，费用应加上$delta_i$。

• 那么我们就算出了新工厂为$now$时符合条件的最优方案，用(运输费用$+h_0+h_{now}$)更新答案即可。

• 外层枚举n个厂址，内层对m个煤矿排序，时间总复杂度为$O(nm\log m)$。

代码如下：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

typedef long long ll;
typedef unsigned long long ull;

int getintRes; 
inline int getint()
{
    static char ch; 
    while ((ch = getchar()) < '0' || ch > '9'); 
    getintRes = ch - '0'; 
    while ((ch = getchar()) >= '0' && ch <= '9')
        getintRes = getintRes * 10 + ch - '0'; 
    return getintRes; 
}

inline void read(int &x)
{
    static char ch; 
    while ((ch = getchar()) < '0' || ch > '9'); 
    x = ch - '0'; 
    while ((ch = getchar()) >= '0' && ch <= '9')
        x = x * 10 + ch - '0'; 
}

inline int getmin(const int &a, const int &b) {return a < b ? a : b;}

const int MaxN = 55; 
const int MaxM = 5e4 + 10; 
const int MaxB = 1e4 + 10; 
const int INF = ~0u >> 1; 

struct cyxPair
{
    int delta, count; 
    cyxPair() {}
    cyxPair(const int &d, const int &c):
        delta(d), count(c) {}
    inline bool operator < (const cyxPair &rhs) const
    {
        return delta < rhs.delta; 
    }
}c[MaxM]; 

int n, m, b; 
int a[MaxM], h[MaxN], c0[MaxM]; 
int minAns = INF, numAns; 

#define p(x, y) cyxPair(x, y)

int main()
{
    read(m), read(b), read(h[0]), read(n); 
    for (int i = 1; i <= m; ++i) read(a[i]); 
    for (int i = 1; i <= n; ++i) read(h[i]); 
    for (int i = 1; i <= m; ++i) read(c0[i]); 
    
    int totCount, totAns, tmp;  
    for (int now = 1; now <= n; ++now)
    {
        static int i; 
        totCount = b, totAns = 0; 
        for (i = 1; i <= m; ++i)
            read(tmp), c[i] = p(c0[i] - tmp, a[i]), totAns += tmp * a[i]; 
        std::sort(c + 1, c + m + 1); 
        for (i = 1; i <= m; ++i)
            if (totCount >= c[i].count)
                totCount -= c[i].count, totAns += c[i].delta * c[i].count; 
            else
                break; 
        if (totCount > 0)
            totAns += totCount * c[i].delta; //当我们有剩余的煤要送但不满该煤矿总量，我们也要将剩下的送出
        totAns += h[0] + h[now]; 
        if (totAns < minAns)
            minAns = totAns, numAns = now; 
    }
    printf("%d\n%d\n", numAns, minAns); 
    return 0; 
}