[HAOI2008] 糖果传递

0
15011418730 LV 7 @ 2025-8-24 21:38:30
自动搬运

查看原文

来自洛谷，原作者为

wyhwyh
这个家伙很菜，什么也没有留下

搬运于2025-08-24 21:38:30，当前版本为作者最后更新于2019-05-19 19:48:44，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

UPD on 2020.4.1: 感谢 OItby 神仙指出错误，已更正。欢迎别的神仙来指教 & 吊打本萌新

首先我们要用到一些均分纸牌的思想(已经理解这种思想的大佬请跳过):

设 $A_i$ 表示第 $i$ 个小朋友原有的糖果数量,

设 $ave$ 表示所有小朋友糖果数量的平均数,

$X_i$ 表示第 $i$ 个小朋友向左传的糖果数量。即：

①如果 $X_i>0:\quad$ 第 $i$ 个小朋友向左传 $X_i$ 个糖果；

②否则如果 $X_i<0:\quad$ 第 $i$ 个小朋友向左传 $|X_i|$ 个糖果。

所以该题的代码为：

Code：
```
#include<cstdio>
int a[101];
int n,x,s;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;++i)
    {
        scanf("%d",&a[i]);
        x+=a[i];
    }
    x/=n;
    for(int i=1;i<n;++i)
    {
        a[i]-=x;
        if(a[i]!=0)
        {
            ++s;
            a[i+1]+=a[i];
        }
    }
    printf("%d",s);
    return 0;
}
```
好现在让我们回到原题糖果传递上来。

看看刚刚设的什么：

设 $A_i$ 表示第 $i$ 个小朋友原有的糖果数量,

$ave$ 表示所有小朋友糖果数量的平均数,

$X_i$ 表示第 $i$ 个小朋友向左传的糖果数量。

则由题可得方程：
$A_1+X_2-X_1=ave$ $A_2+X_3-X_2=ave$ $···$ $A_n+X_1-X_n=ave$
即：

$A_i+X_{i+1}-X_i=ave(1\le i<n)$

$A_n+X_1-X_n=ave(i=n)$

变形得：
$X_2=ave+X_1-A_1$ $$X_3=ave+X_2-A_2=ave+(ave+X_1-A_1)-A_2=2ave-A_1-A_2+X_1 $$ $···$ $X_1=ave+X_n-A_n=n·ave-A_1-A_2-…-A_n+X_1$
这时我们设:
$C_1=A_1-ave$ $C_2=A_1+A_2-ave$ $···$ $C_n=A_1+A_2+…+A_n-n·ave$
即设：

$C_i=\sum_{j=1}^iA_j-i·ave(1\le i\le n)$

则有:
$X_2=X_1-C_1$ $X_3=X_1-C_2$ $···$ $X_n=X_1-C_n$
即：

$X_i=X_1-C_i$

这时我们返回来看所求,要求传递价值最小，

这就是说，要求最小化
$|X_1|+|X_2|+···+|X_n|$
而该式等于
$|X_1-C_1|+|X_1-C_2|+···+|X_1-C_n|$
即求:

$$MIN \{ \sum_{i=1}^nX_i \}=MIN \{ \sum_{i=1}^nX_1-C_i \} $$

这样就好办了， $C_i$ 是已知（额，至少是可以预处理出来）的，要想最小化上式，我们把 $C_i$ 看成数轴上的一个个点，现在问题就转化成了找出一个点 $X_1$ ，使得她到各个 $C_i$ 上的点的距离和最小。

而这个点就是这 $n$ 个点的中位数，后面有证明qwq

那么求出了 $X_1$ 之后，根据
$X_2=X_1-C_1$ $X_3=X_1-C_2$ $···$ $X_n=X_1-C_n$
这一坨柿子，我们可以求出 $X_2,X_3…X_n$ ,然后就可以偷税的得到所求的：

最小化
$|X_1|+|X_2|+···+|X_n|$
啦233~~~

代码好丑，大家别嫌弃qwq：

Code：
```
#include<bits/stdc++.h>
#define max(a,b) a>b?a:b
#define min(a,b) a<b?a:b
#define inline il

typedef long long ll;
typedef long double ld;

const int inf = 0x7fffffff;
const int N = 1e6+1;

ll n;
ll a[N],c[N];
ll ave,ans,mid;

using namespace std;

int main()
{
	scanf("%lld",&n);
	for(int i=1;i<=n;++i)
		scanf("%lld",&a[i]),ave+=a[i];
	ave/=n;
	for(int i=1;i<=n;++i)
		c[i]=c[i-1]+ave-a[i-1];
	sort(c+1,c+n+1);
	mid=c[(n+1)/2];
	for(int i=1;i<=n;++i)
		ans+=abs(mid-c[i]);
	printf("%lld",ans);
	return 0;
}
```
附：数学证明

在数轴上有 $n$ 个点，找出一个点 $x$ ，使得她到各个点的距离和最小。

求证：该点表示的数就是这 $n$ 个数的中位数。

如果我们把数轴上的点两两配对，最大的配最小的，次大的配次小的……

则到每组点最近的距离的点在这两个点中间，那么

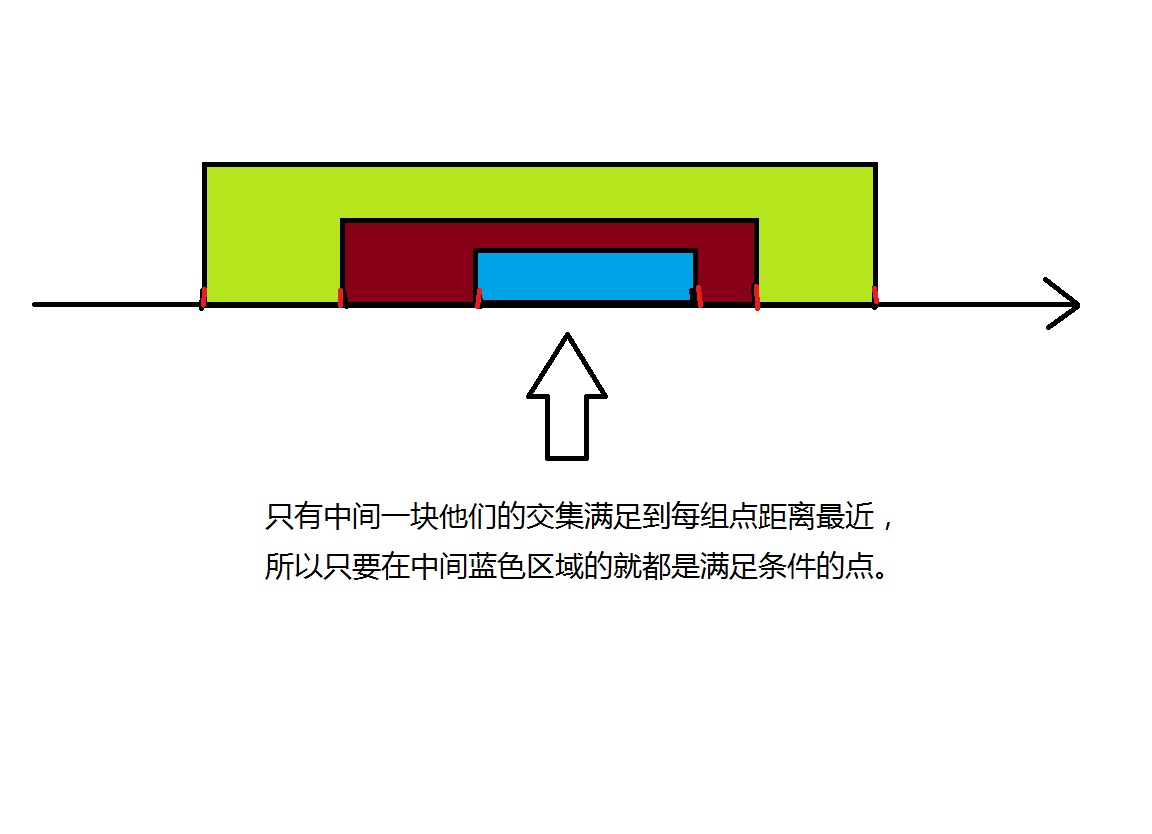
如果有奇数个点，那么显然中间那个点便为所求。

**∴**该点表示的数是这 $n$ 个数的中位数得证。

注：

有一些柿子在文中以不同的形式重复出现，主要是为了同时满足大佬和蒟蒻的需要。一些前面写了‘即…’并用

这个东西

框起来的一般是适合大佬的较严（bian）格（tai）数学写法，而其他的则是简明易懂的正常的、不变态的写法。