自动搬运

查看原文

来自洛谷，原作者为

	pufanyi pufanyi.github.io

搬运于2025-08-24 21:38:28，当前版本为作者最后更新于2018-05-27 13:49:46，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

两页的爆蛋记录（来自蒟蒻的无助）。

orz 千古神犇 wzp 一眼秒题。

这种题一定要耐心地做（初中数学老师一直这么对我说）。

首先，我们来看其简化版：

我们把 $\odot B$ 覆盖在 $\odot A$ 上，我们发现我们需要求出 $\angle A$ 的度数。我的方法是连结 $CB,AB,BD,AB$（如图）。我们发现 $\triangle ABC\cong\triangle ABD$，又在 $\triangle ABC$ 中，由余弦定理得：$\cos A=\frac{{AC}^2 + {AB}^2 - BC^2}{2\times AB \times AC}$ 于是我们就得到了 $\angle A$。

恭喜你过了样例。

double dist = get_dist(A, B);
if(dist > A.r+B.r || A.r + dist < B.r)
	return;
if(dist + B.r < A.r)//完全被覆盖
{
	gaif = true;//标记直接跳出
	return;
}
double alpha = acos((sqr(B.r)+sqr(dist)-sqr(A.r))/(B.r*dist*2.));

那么如果有多个圆呢？

我们发现，对于 $\odot A$ 来说，$EF$ 被覆盖了两次，但我们之能减一次。于是我们就想到了：对于每个圆，枚举盖在其上面的圆，算出每个覆盖“线段”的左右端点，然后进行一次线段覆盖将其合并。最后，我们只要算出没有被覆盖到的线段长度即可。

我们用极角来表示圆上点的位置，这样我们就可以进行线段覆盖操作了。

如图，$AE$ 平行 $x$ 轴，我们以算出 $AC$ 的斜率，加个 $\arctan$ 即可求出 $\angle CAE$，然后 $\angle EAD$、$\angle BAE$ 均可求出。

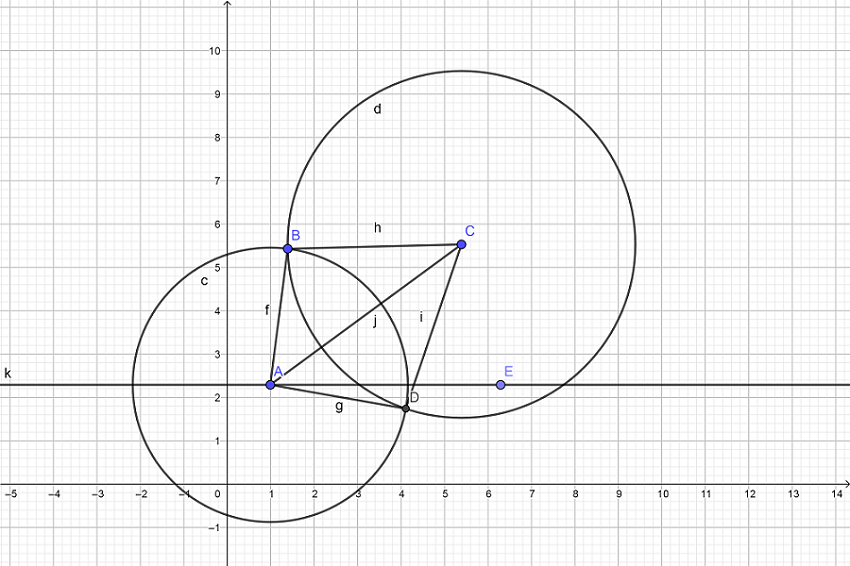
于是理论上的问题就全部解决了。

对于极角还有一个小细节：

由于我们在线段求并时只容许有$1$到$2\pi$的弧度，因此，对于两个“交点”$l,r$，我们需要作出以下特判：

1. $l<0$ 且 $r<0$ 时，我们要把 $l$ 与 $r$ 均加上 $2\pi$；
2. $l<0$ 且 $r>0$ 时，我们插入 $[l+2\pi,2\pi],[0,r]$ 两段；
3. $l<2\pi$ 且 $r>2\pi$ 时，我们插入 $[l,2\pi],[0,r-2\pi]$ 两段。

具体代码实现如下：

//const pi2 = 2*pi

if(jiao1 < 0 && jiao2 < 0)//这句话花了我一页的提交
{
	jiao1 += pi2, jiao2 += pi2;
}
if(jiao1 >= 0 && jiao2 <= pi2)
	cha(jiao1, jiao2);
else
{
	if(jiao1 < 0)
	{
		cha(jiao1+pi2, pi2);
		cha(0, jiao2);
	}
	else
	{
		cha(jiao1, pi2);
		cha(0, jiao2-pi2);
	}
}

整体代码

//代码有些冗长，大佬勿喷
//蒟蒻无毒，请放心食用

#include <cstdio>
#include <cmath>
#include <algorithm>

using namespace std;

const int maxn = 10005;
const double pi = 3.1415926535897932;
const double pi2 = 2*pi;

struct Point
{
	double x, y;
};

inline double sqr(double x)
{
	return x*x;
}

inline double get_dist(Point x, Point y)
{
	return sqrt(sqr(x.x-y.x) + sqr(x.y-y.y));
}

struct Circle
{
	Point O;
	double r;
} c[maxn];

inline double get_dist(Circle x, Circle y)
{
	return get_dist(x.O, y.O);
}

int n;

struct Fugai
{
	double l, r;

	inline bool operator < (const Fugai& other) const
	{
		return l < other.l;
	}
} fugai[maxn];

int nown;
inline void cha(double l, double r)
{
	fugai[++nown] = (Fugai)
	{
		l, r
	};
}

bool gaif = false;//gaif = true表示该圆盘被上面的大圆盘完全覆盖

inline void jiao(Circle A, Circle B)
{
	double dist = get_dist(A, B);
	if(dist > A.r+B.r || A.r + dist < B.r)//没有任何覆盖
		return;
	if(dist + B.r < A.r)//如果被一个大圆盘完全覆盖，直接跳出
	{
		gaif = true;
		return;
	}
	double alpha = acos((sqr(B.r)+sqr(dist)-sqr(A.r))/(B.r*dist*2.));//上图中的角CAD
	double beta = atan2(A.O.y-B.O.y, A.O.x-B.O.x);//上图中的角CAE
	double jiao1 = beta-alpha;//线段覆盖中的l
	double jiao2 = beta+alpha;//线段覆盖中的r
	if(jiao1 < 0 && jiao2 < 0)//对极角的一些特判
	{
		jiao1 += pi2, jiao2 += pi2;
	}
	if(jiao1 >= 0 && jiao2 <= pi2)
		cha(jiao1, jiao2);
	else
	{
		if(jiao1 < 0)
		{
			cha(jiao1+pi2, pi2);
			cha(0, jiao2);
		}
		else
		{
			cha(jiao1, pi2);
			cha(0, jiao2-pi2);
		}
	}
}

inline double get_ans()
{
	double ans = 0;
	sort(fugai+1, fugai+nown+1);
	double lastr = fugai[1].l;
	for(int i = 1; i <= nown; ++i)
	{
		if(lastr >= fugai[i].r)
			continue;
		if(fugai[i].l > lastr)
			ans += fugai[i].r - fugai[i].l;
		else
			ans += fugai[i].r - lastr;
		lastr = fugai[i].r;
	}
	return ans;
}

int main()
{
	scanf("%d", &n);
	for(int i = 1; i <= n; ++i)
		scanf("%lf%lf%lf", &c[i].r, &c[i].O.x, &c[i].O.y);
	double ans = 0;
	for(int i = n; i; --i)
	{
		nown = 0;
		for(int j = n; j > i; --j)//枚举所有该圆盘之后的圆盘
		{
			jiao(c[j], c[i]);
			if(gaif)
				break;
		}
		if(gaif)
			gaif = false;
		else
			ans += (pi2-get_ans())*c[i].r;
		nown = 0;
	}
	printf("%.3f", ans);
	return 0;
}