自动搬运

查看原文

来自洛谷，原作者为

	学委 希望以后某时候还能来写题！

搬运于2025-08-24 21:38:23，当前版本为作者最后更新于2018-09-30 15:16:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

（其实我主要想来讲第二问算法的另一个证明）

第一问

如果要保留 $a[i]$ 和 $a[j]$，前提是：他们中间的数本身就合法，或者他们中间的数可以被改成合法。

比如，17，50，50，50，19这个序列，看上去17和19能保留，但如果保留，中间三个50怎么改都不会单调上升。

可见只有 $a[j]$ 和 $a[i]$ 的差大于等于 $j-i$ 才允许同时保留两者，否则中间一定出错。

$a[j] - a[i] >= j - i$ 移项：

$a[j] - j >= a[i] - i$，此为保留条件。

所以把根据 $a$ 预处理出新序列 $b[i] = a[i] - i$，然后找 $b$ 的最长不下降子序列的长度，就是最多能保留的个数。

第二问

把 $a$ 变成严格单调上升序列等同于：在 $b$ 上对应地处理，并把 $b$ 变成单调不降。现在就考虑 $b$ 怎么改才能代价最小。

注意：（一）$b$ 的最长不下降子序列可能有多个。

（二）$b$ 的最长不下降子序列中，任何两个相邻的元素 $b[i], b[j]$（相邻指的是在子序列中相邻，而在 $b$ 中不一定相邻） 之间，绝对不存在另一个大小介于两者之间的元素。否则取这个元素，保证合法，而且可以使不降序列更长。

所以每个被保留的 $b[i]$ 和 $b[j]$ 之间的元素全部不合法。怎么改变这两者之间的元素？（这是个子问题）好像有一大堆方法。

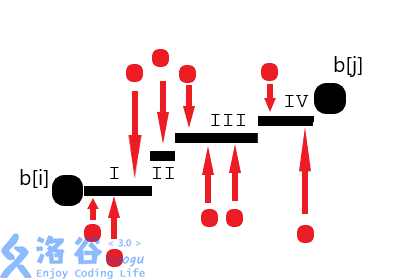
黑线表示修改以后的海拔。显然所有方法都是阶梯（横线看作台阶）。此方法看上去很糟。观察，区间 $II$ 内有一个强制拉低的点，我们可以放宽要求，提高到 $III$ 那么高。

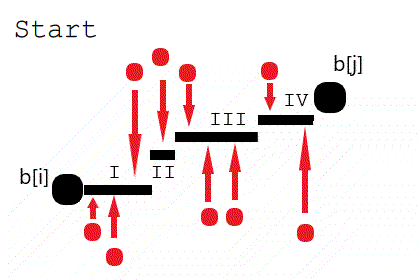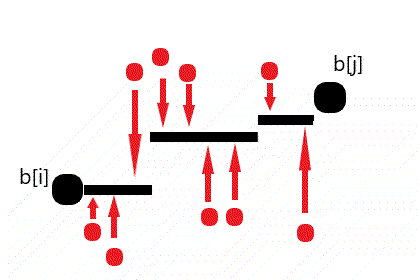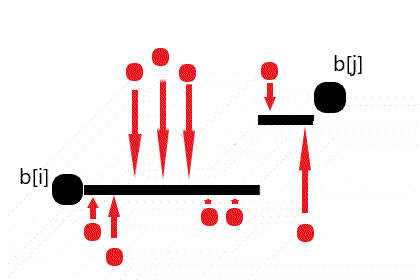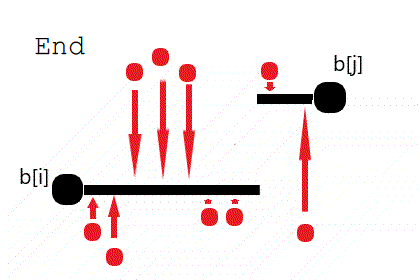
对于子问题的任何一种处理法，我们可以把其中一块台阶这样变化：**如果台阶上的“上升点数目”大于“下降点数目”，那么把台阶下降（以满足那么多“上升点”的要求！），直到它下降到和左边台阶一样高，也就和左边变成了同一块台阶。**反之，就把台阶上升到和右边台阶一样高。然后继续缩减台阶。如果有Up = Down的，则台阶向上向下都可以（代价不变，台阶数目减少）。

这个过程始终保证合法、保证代价减小或不变。

这样变化到End，一定只剩下两块台阶，左边的高 $b[i]$，右边的高 $b[j]$。

以上说明，最优解一定是（或者说，一定可以是）

左边 $b[i] ~to~ b[k]$ 全部变成 $b[i]$ 且

右边 $b[k+1] ~to~ b[j]$ 全部变成 $b[j]$

的形态。如果最优解不是这样，我们可以无偿甚至减偿来变成这种形态。

每个区间的 $k$ 可以枚举。

#include <cstdio>
#include <cctype>
#include <cstring>
inline int getint()
{
	int res = 0, neg = 0, ch = getchar();
	//亲测多种手写isdigit都比<cctype>的isdigit慢
    //更快者欢迎私信 
	while(!(isdigit(ch) || ch == '-') && ch != EOF)
		ch = getchar();
	if(ch == '-')
		neg = 1;
	while(isdigit(ch))
		res = (res << 3) + (res << 1) + (ch - '0'), ch = getchar();
	return neg ? -res : res;
}
#define re register
#define LL long long
#define INF 2147483647
inline LL min(LL x, LL y) {return x < y ? x : y; }
inline LL abs(LL x) {return x < 0 ? -x : x; }
//inline也才比<algorithm>快一点。宏定义日常写挂

int n;
int a[40010], b[40010];
int Minof[40010], len = 0, Longest[40010];

int first[40010], to[40010], nxt[40010], cnt = 0;
LL f[40010];
LL sumL[40010], sumR[40010];

inline void addE(int u, int v)
{
	++cnt;
	to[cnt] = v;
	nxt[cnt] = first[u];
	first[u] = cnt;
}

int main()
{
	n = getint();
	for(re int i = 1; i <= n; ++i)
		a[i] = getint(), b[i] = a[i]-i;
	//想要保留i和j，前提是他们中间能好好放东西 
	//保留的数目越多越好
	
	b[n+1] = INF;
	for(re int i = 1; i <= n+1; ++i)
	{
		int l = 0, r = len;
		while(l < r)
		{
			int mid = (l + r + 1) >> 1;
			if(Minof[mid] <= b[i])
				l = mid;
			else
				r = mid - 1;
		}
		if(l == len) 
			++len;
			
		Longest[i] = l+1;
		addE(Longest[i], i);
		//以i结尾的最长不降子序列长度为Longest[i]。
		//如果b[j]想拼上合适的b[i]，就去前面找长度为Longest[b[j]]-1且能接上的。
		//因此要记录各个长度的子序列的结尾。用vector会更直观

		Minof[l+1] = b[i];
	}
	addE(0, 0);//这么做因为：长度为1的最长不下降子序列的前面几个数也要处理 
	printf("%d\n", n-(len-1));
	
	memset(f, 20, sizeof(f));
	
	b[0] = -INF; //将自动处理“真正的最长不降子序列”前面的几个数 
	f[0] = 0;//把前i个数，改成单调不降子序列且该序列以i结尾的最小代价
	for(re int i = 1; i <= n+1; ++i)//末尾多一个INF，然后依然是把序列变成不下降，
	//将自动处理“真正的最长不降子序列”的后面几个数（也要改啊） 
	{
		for(re int p = first[Longest[i]-1]; p; p = nxt[p])//枚举长度为“b[j]的长度-1”的所有b[i] 
		{
			int u = to[p];
			if(u > i || b[u] > b[i])//嗯，虽然它的长度确实是“我的长度-1”，但可能我并不能接在它后面 
				continue;
			
			//下面注意利用前缀和 
			sumL[u] = 0;//最小代价形态在“i____--------j” 
			for(re int k = u+1; k <= i-1; ++k)
				sumL[k] = sumL[k-1] + abs(b[k] - b[u]);
			//u+1 to k     
			
			//k+1 to i-1
			sumR[i-1] = 0;
			for(re int k = i-2; k >= u; --k)
				sumR[k] = sumR[k+1] + abs(b[k+1] - b[i]);
			//这里求前缀和的时候要弄清楚…… 
			
			for(re int k = u; k <= i-1; ++k)
				f[i] = min(f[i], f[u] + sumL[k] + sumR[k]);
		}	
	}
	//题解看懂，但后半段代码看不懂就打个记忆化搜索好了 
	
	printf("%lld\n", f[n+1]);
	return 0;
}

有你不明白或者我写错的可评论，这样包括评论区就是一篇动态题解了。