自动搬运

查看原文

来自洛谷，原作者为

	TKXZ133 竭诚则胡越为一体，傲物则骨肉为行路

搬运于2025-08-24 21:38:21，当前版本为作者最后更新于2023-07-19 21:27:53，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

基站建设

题目大意

在平面上存在 $n$ 个点，第 $i$ 个点的坐标为 $(x_i,0)$，具有一个发射半径 $r_i$ 和一个费用 $v_i$。

连接具有方向性，当且仅当 $j<i$ 且点 $i$ 的接收范围与点 $j$ 的发射范围相切时点 $i$ 才能连接到点 $j$。

第 $i$ 个点的发射范围是指一个圆心在 $(x_i,r_i)$，半径为 $r_i$ 的圆，接收范围是指一个圆心在 $(x_i,r_i')$，半径为 $r_i'$ 的圆，其中 $r_i'$ 可以被指定。

点 $i$ 连接到点 $j$ 的代价被定义为 $\sqrt{r_i'}+v_i$，连接具有按方向的传递性，也就是说，若 $a$ 连接到 $b$，$b$ 连接到 $c$，那么 $a$ 也连接到 $c$。

平面上还存在一个特殊点 $u$，点 $u$ 连接到点 $j$ 的条件是 $x_j+r_j\ge m$，且没有代价。求将点 $u$ 连接到点 $1$ 的最小代价。

思路分析

斜率优化 DP 好题。

设 $f_i$ 表示考虑到第 $i$ 个点，第 $i$ 个点强制连接到某个点的最小代价。

考虑初值，有 $f_1=v_1$。考虑终值，所求即 $\min\limits_{x_i+r_i\ge m} f_i$。

枚举第 $i$ 个点连接到的点 $j$，容易得状态转移方程为：

$$f_i=\min_{j<i}(f_j+w(i,j))$$

其中，$w(i,j)$ 表示将点 $i$ 和点 $j$ 连接的代价，即 $r_i'+v_i$。

$r_i'$ 可以直接计算出来，根据勾股定理，有 $(r_i'-r_j)^2+(x_i-x_j)^2=(r_i'+r_j)^2$，容易解得 $r_i'=\frac{(x_i-x_j)^2}{4r_j}$。

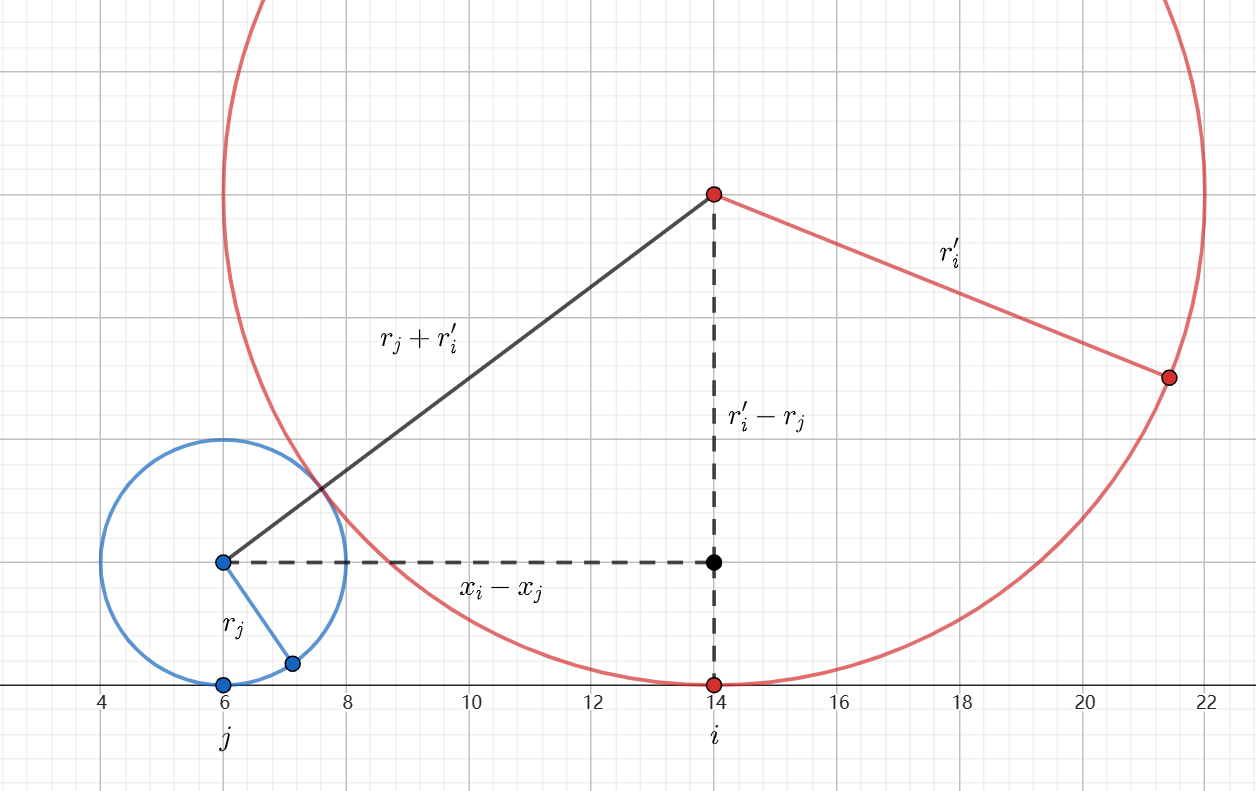
故 $w(i,j)=\frac{x_i-x_j}{2\sqrt{r_j}}+v_i$。

代入原方程，则：

$$f_i=\min_{j<i}(f_j+\frac{x_i-x_j}{2\sqrt{r_j}}+v_i) $$

然后是常规斜率优化化简：

$$\begin{aligned}f_i&=f_j+\frac{x_i}{2\sqrt{r_j}}-\frac{x_j}{2\sqrt{r_j}}+v_i\\(f_i-v_i)&=(\frac{1}{2\sqrt{r_j}})(x_i)+(f_j+\frac{x_j}{2\sqrt{r_j}})\end{aligned} $$

设：

$$\begin{cases}y=f_i-v_i\\k=\frac{1}{2\sqrt{r_i}}\\x=x_i\\b=f_j+\frac{x_j}{2\sqrt{r_j}}\end{cases} $$

问题转化为每次插入一条 $k_i=\frac{1}{2\sqrt{r_i}},b_i=f_i+\frac{x_i}{2\sqrt{r_i}}$ 的直线，查询 $x=x_i$ 处的最小值，用李超线段树优化即可。

考虑到 $x_i$ 的值域较大，可以对其离散化。

代码

#include <iostream>
#include <cstring>
#include <cmath>
#include <cstdio>
#include <algorithm>

using namespace std;
#define int long long
const int N=500500;
#define inf 1e18
#define mid ((l+r)>>1)

int n,m;
int x[N],bx[N],r[N],v[N];

double f[N],ans=inf;

struct Line{
    double k,b;
}line[N];

double calc(int id,int pos){//计算第 id 条直线在离散化后的 pos 处的值
    return line[id].k*bx[pos]+line[id].b;
}

bool Less(int id1,int id2,int pos){//比较两条直线的优劣
    return calc(id1,pos)<calc(id2,pos);
}

struct ST{//简洁的李超线段树
    int a[N<<2];
    void add(int p,int l,int r,int id){
        if(l==r){if(Less(id,a[p],l)) a[p]=id;return ;}
        if(Less(id,a[p],mid)) swap(a[p],id);
        if(Less(id,a[p],l)) add(p<<1,l,mid,id);
        if(Less(id,a[p],r)) add(p<<1|1,mid+1,r,id);
    }
    double query(int p,int l,int r,int pos){
        double res=calc(a[p],pos);
        if(l==r) return res;
        if(pos<=mid) res=min(res,query(p<<1,l,mid,pos));
        else res=min(res,query(p<<1|1,mid+1,r,pos));
        return res;
    }
}tree;

signed main(){
    scanf("%lld%lld",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%lld%lld%lld",&x[i],&r[i],&v[i]);
        bx[i]=x[i];
    }
    int tot=unique(bx+1,bx+n+1)-bx-1;
    for(int i=1;i<=n;i++)
        x[i]=lower_bound(bx+1,bx+tot+1,x[i])-bx;//常规离散化
    line[0]={0,inf};//将第 0 条线的值赋为无穷，可以省去特判空直线的情况
    f[1]=v[1];//初始化
    line[1]=Line{1/(2*sqrt(r[1])),f[1]-bx[x[1]]/(2*sqrt(r[1]))};
    tree.add(1,1,n,1);//插入第一条直线
    for(int i=2;i<=n;i++){
        f[i]=tree.query(1,1,n,x[i])+v[i];
        line[i]=Line{1/(2*sqrt(r[i])),f[i]-bx[x[i]]/(2*sqrt(r[i]))};
        tree.add(1,1,n,i);//插入直线
    }
    for(int i=1;i<=n;i++)
        if(bx[x[i]]+r[i]>=m) ans=min(ans,f[i]);//对所有满足条件的点取最小值
    printf("%.3lf\n",ans);
    return 0;
}