1 条题解
-
0
自动搬运
来自洛谷,原作者为
Rhodoks
一旦尝试过飞行的滋味,便会永远仰望天空。因为你曾去过那里,并且渴望回到那里。搬运于
2025-08-24 21:38:20,当前版本为作者最后更新于2019-02-21 20:28:15,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
新学虚树,写篇文章仔细地回顾一下吧。。。这玩意花了挺长时间的。
什么是虚树
虚树常常被使用在树形中,就比如这题。当一次询问仅仅涉及到整颗树中少量结点时,为每次询问都对整棵树进行在时间上是不可接受的。此时,我们建立一颗仅仅包含部分关键结点的虚树,将非关键点构成的链简化成边或是剪去,在虚树上进行。
虚树包含所有的询问点及它们之间的。显然虚树的叶子节点必然是询问点,因此对于某次含有个点的询问,虚树最多有个叶子结点,从而整颗虚树最多只有个结点(这会在虚树变成二叉树形态时达到)。
建立虚树之前
我们需要:
预处理出原树的序以及可能用到的一些其他东西。
高效的在线算法,单次询问的倍增和树剖,的皆可。
将询问点按序排序。
如何建立虚树
最右链是虚树构建的一条分界线,表明其左侧部分的虚树已经完成构建。我们使用栈来维护所谓的最右链,为栈顶位置。值得注意的是,最右链上的边并没有被加入虚树,这是因为在接下来的过程中随时会有某个插到最右链中。
初始无条件将第一个询问点加入栈中。
将接下来的所有询问点顺次加入,假设该询问点为,为该点和栈顶点的最近公共祖先即。
由于是的祖先,必然在我们维护的最右链上。
考虑和及栈中第二个元素的关系。
情况一
,也就是说,在的子树中
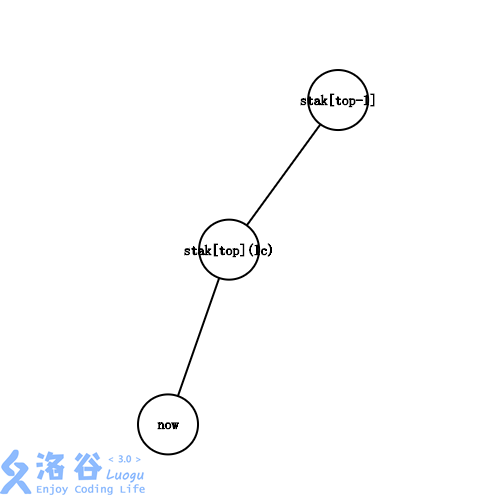
这时候,我们只需把入栈,即把它加到最右链的末端即可。
情况二
在和之间。
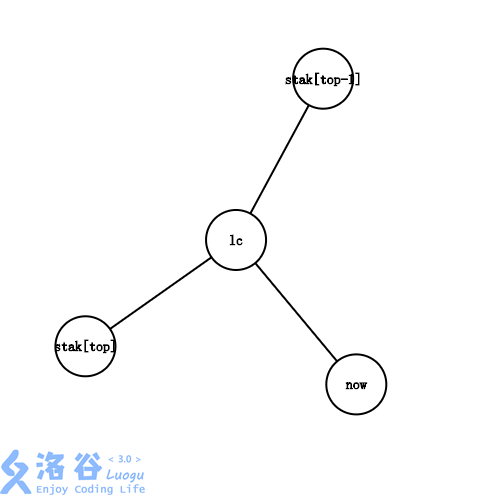
显然,此时最右链的末端从变成了,我们需要做的,首先是把边加入虚树,然后,把出栈,把和入栈。
情况三
。
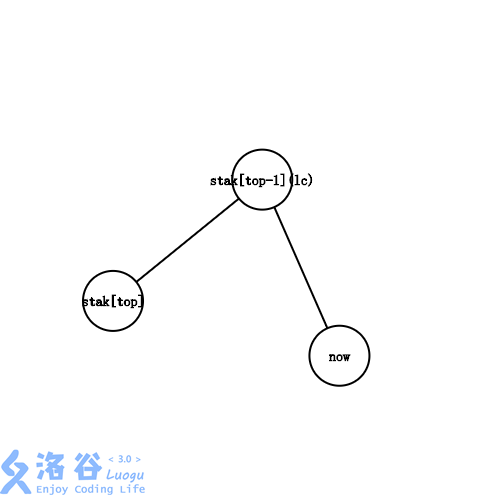
这种情况和第二种情况大同小异,唯一的区别就是不用入栈了。
情况四
此时有。已经不在的子树中了,甚至也未必在的子树中。
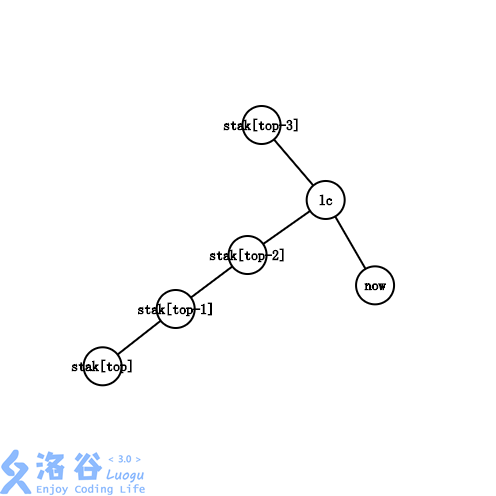
以图中为例,最右链从变成了。我们需要循环依次将最右链的末端剪下,将被剪下的边加入虚树,直到不再是情况四。
就上图而言,循环会持续两轮,将依次出栈,并且把边加入虚树中。随后通过情况二完成构建。
当最后一个询问点加入之后,再将最右链加入虚树,即可完成构建。
一些问题
- 如果栈中仅仅有一个元素,此时是否会出问题?
对于栈,我们从开始储存。那么在这种情况下,,并且。此时恒成立。也就是说,扮演了深度最小的哨兵,确保了程序只会进入情况一和二。
- 如何在一次询问结束后清空虚树?
不能直接对图进行清空,否则复杂度会退化到的复杂度,这是我们无法承受的。在的过程中每当访问完一个结点就进行清空即可。
回到本题
以样例的询问二为例(如下图)
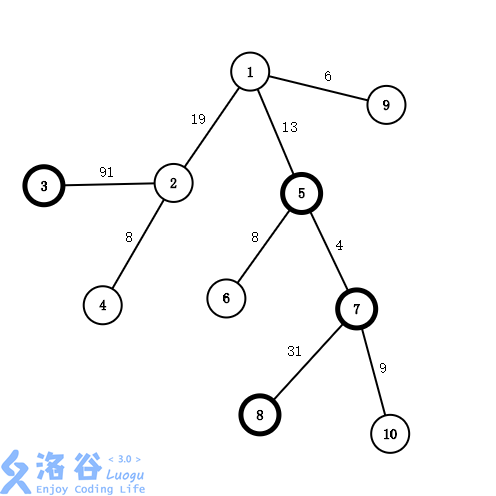
建立虚树是长这个样子的
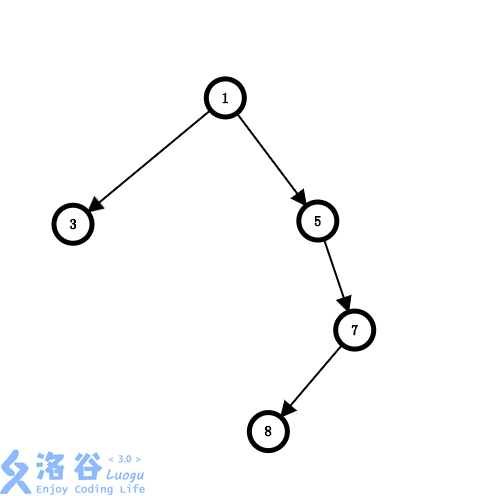
在本题中,建立有向树即可。我们预处理出代表从到路径上最小的边权。如果是询问点,那么切断及其子树上询问点的最小代价,否则,最小代价(其中是的儿子)。值得注意的是,即使是询问点,按道理用不到的值,但仍旧需要对其儿子进行,因为清空虚树需要对整个虚树进行遍历。
还有答案会爆,所以不仅数组要开,初始化的也有必要开得足够大。我一开始直接拿结果了最后一个点。。。。
最后就是蒟蒻
码风清奇常数巨大命名混乱的代码了#include <bits/stdc++.h> #define INL inline #define REG register #define DB double #define LDB long double #define ULL unsigned long long #define LL long long #define RPT(i,x,y) for (REG int i=x;i<y;i++) #define DRPT(i,x,y) for (REG int i=x;i>y;i--) #define MST(a,b) memset(a,b,sizeof(a)) #define MAXN 500500 #define MAXM 10000 #define MOD 998244353 #define INF 0x3f3f3f3f #define LLINF 0x3f3f3f3f3f3f3f3f #define EPS 1e-5 #define _ 0 using namespace std; int dfn[MAXN]; int dep[MAXN]; int fa[MAXN][25]; LL minv[MAXN]; int m[MAXN]; int lst[MAXN]; bool query[MAXN]; int n,q; int num; int top; int dfscnt=1; int stak[MAXN]; struct EDGE { int to,next; LL val; }edge[MAXN<<1],edge1[MAXN<<1]; int head[MAXN];//初始图存储 int cnt=1; INL void add(int x,int y,LL v) { edge[cnt].next=head[x]; edge[cnt].to=y; edge[cnt].val=v; head[x]=cnt++; } int head1[MAXN];//虚树存储 int cnt1=1; INL void add1(int x,int y) { edge1[cnt1].next=head1[x]; edge1[cnt1].to=y; head1[x]=cnt1++; } void dfs(int pos) { int k; for (k=0;fa[pos][k];k++) fa[pos][k+1]=fa[fa[pos][k]][k]; m[pos]=k; dfn[pos]=dfscnt++; for (int i=head[pos];i;i=edge[i].next) { REG int to=edge[i].to; if (!dfn[to]) { dep[to]=dep[pos]+1; minv[to]=min(minv[pos],edge[i].val); fa[to][0]=pos; dfs(to); } } } LL dfs1(int pos) //dp { LL sum=0; LL tem; for (int i=head1[pos];i;i=edge1[i].next) { int to=edge1[i].to; sum+=dfs1(to); } if (query[pos]) tem=minv[pos]; else tem=min(minv[pos],sum); query[pos]=false; //清空虚树 head1[pos]=0; return tem; } int lca(int x,int y) //倍增LCA { if (dep[x]<dep[y]) swap(x,y); DRPT(i,m[x],-1) if (dep[fa[x][i]]>=dep[y]) x=fa[x][i]; if (x==y) return x; DRPT(i,m[x],-1) if (fa[x][i]!=fa[y][i]) { x=fa[x][i]; y=fa[y][i]; } return fa[x][0]; } bool cmp(int x1,int x2) { return dfn[x1]<dfn[x2]; } int main() { minv[1]=LLINF; cin>>n; int x,y; LL v; RPT(i,0,n-1) { scanf("%d%d%lld",&x,&y,&v); add(x,y,v); add(y,x,v); } dfs(1); cin>>q; while (q--) { cin>>num; RPT(i,1,num+1) { scanf("%d",&lst[i]); query[lst[i]]=true; } sort(lst+1,lst+num+1,cmp); stak[top=1]=lst[1]; RPT(i,2,num+1) { int now=lst[i]; int lc=lca(now,stak[top]); while (1) if (dep[lc]>=dep[stak[top-1]]) { if (lc!=stak[top]) //不满足该条件为情况一 { add1(lc,stak[top]); if (lc!=stak[top-1]) //情况二 stak[top]=lc; else //情况三 top--; } break; } else //情况四 { add1(stak[top-1],stak[top]); top--; } stak[++top]=now; //最后统一把now压进栈中 } while (--top) add1(stak[top],stak[top+1]); //将最右链放进虚树 cout<<dfs1(stak[1])<<endl; cnt1=1; } return ~~(0^_^0); }第一次写那么长的题解,
以上内容均为口胡。由于自己实在是太蒟蒻了,错误缺漏之处在所难免,如有发现烦请各位大佬们指正。
- 1
信息
- ID
- 1533
- 时间
- 2000ms
- 内存
- 505MiB
- 难度
- 6
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
