自动搬运

查看原文

来自洛谷，原作者为

	Owen_codeisking 前OIer/ACMer/柚子厨/酒姬民

搬运于2025-08-24 21:38:10，当前版本为作者最后更新于2018-09-19 19:14:59，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

刚刚一看这题，感觉很水，结果一直$95$分……没有特判，$GG$

题目大意：求$G^{\sum{d|n\ C_n^d}}\ mod\ 999911659$

思路与其他题解相像，考虑到$999911659$是质数，那么就用欧拉定理的推论得：

$$G^{\sum{d|n\ C_n^d}}\ mod\ 999911659=G^{\sum{d|n\ C_n^d\ mod\ 999911658}}\ mod\ 999911659 $$

那么关键计算$\sum{d|n\ C_n^d}\ mod\ 999911658$.直接$Lucas$绝对挂，那么尝试把模数缩小再合并

将$999911658$因数分解，可得$999911658=2\times 3\times 4679\times 35617$.那么把模数缩小，枚举$n$的因数$d$，然后运用$Lucas$定理把$C_n^d$算出来，分别计算出$\sum{d|n\ C_n^d}$对$2,3,4679,35617$四个质数取模的结果，记为$a_1,a_2,a_3,a_4$.

最后，用中国剩余定理求解一下方程组：

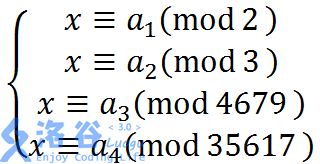
然后就得到了最小的非负整数解$x$，之后用快速幂求一下$G^x$就得到答案

中间的图片是我$latex$不会打用$windows$自带$mip$截图的，有个水印懒得找图床

顺带说一句，欧拉定理$a^b\equiv m(mod\ p)$，当且仅当$(a,p)=1$

$upd:2019.06.19$

开头那句是我那时一时中二写上去的……不要在意

我感觉当时还没有讲清楚，$Lucas$ 的复杂度是 $O(p\log_p n)$，所以缩小模数降下时间就可以了。

$Code\ Below:$

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int mod=999911658;
LL n,G,farc[50010],a[5],b[5]={0,2,3,4679,35617},val;

LL fast_pow(LL a,LL b,LL p)//快速幂
{
	LL ret=1;
	for(;b;b>>=1,a=a*a%p)
		ret=ret*(b&1?a:1)%p;
	return ret;
}

void init(LL p)//预处理
{
	farc[0]=1;
	for(LL i=1;i<=p;i++)
		farc[i]=farc[i-1]*i%p;
}

LL C(LL n,LL m,LL p)//组合数
{
	if(n<m) return 0;
	return farc[n]*fast_pow(farc[m],p-2,p)%p*fast_pow(farc[n-m],p-2,p)%p;
}

LL Lucas(LL n,LL m,LL p)//Lucas定理
{
	if(n<m) return 0;if(!n) return 1;
	return Lucas(n/p,m/p,p)*C(n%p,m%p,p)%p;
}

void CRT()//中国剩余定理
{
	for(LL i=1;i<=4;i++)
		val=(val+a[i]*(mod/b[i])%mod*fast_pow(mod/b[i],b[i]-2,b[i]))%mod;
}

int main()
{
	scanf("%lld%lld",&n,&G);
	if(G%(mod+1)==0){
		printf("0\n");
		return 0;
	}//特判
	for(LL k=1;k<=4;k++){
		init(b[k]);
		for(LL i=1;i*i<=n;i++){
			if(n%i==0){
				a[k]=(a[k]+Lucas(n,i,b[k]))%b[k];
				if(i*i!=n){
					a[k]=(a[k]+Lucas(n,n/i,b[k]))%b[k];
				}
			}
		}
	}//逐一枚举n的约数
	CRT();
	printf("%lld\n",fast_pow(G,val,mod+1));//注意mod要+1
	return 0;
}