自动搬运

查看原文

来自洛谷，原作者为

	Orion545 **

搬运于2025-08-24 21:36:59，当前版本为作者最后更新于2018-04-21 12:01:41，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

广告

蒟蒻のblog

更新现场（建议先看“思路”开始的部分）

鉴于评论区的大家对代码中的$ans$提出的疑惑，我再重新细讲一遍

考虑$kmp$过程中求出的$next$数组，也就是我的代码里面的$fail$

实际上这些$fail$作为边的话，它们构成了一个树形结构。这个树形结构就是KMP自动机的$fail$树（关于$fail$树的概念可以参考$AC$自动机，这里实际上$KMP$自动机就是在$AC$自动机只插入了一个字符串的情况下建立的自动机，同理它也拥有$fail$树）（同时也要注明，实际上此处使用的应该是$MP$算法而不是$KMP$算法，所以称之为$MP$自动机更合适）

那么理解了这个以后，就可以轻松意识到，代码里面的$ans$实际上是这个节点在$fail$树上的深度

应当意识到，由于对于前缀$i$而言，$next[i]$、$next[next[i]]$、$next[next[next[i]]]$等等都是它的公共前后缀，所以节点$i$在该字符串的$KMP$自动机的$fail$树上的深度就是前缀$[1,i]$的公共前后缀个数

在后面的递归求解过程中，如果把这个过程放到$fail$树上理解，同样会好理解很多：$j$也就是在$fail$树上往前跳的过程中用于记录的一个指针，它会每次跳到直到$j\ast 2>i$为止

思路

首先，这题最好的一个地方，在于它给出的关于$next$的讲解实在是妙极......甚至可以说我的kmp是过了这道题以后才脱胎换骨的

然后是正文：

如何求$num$数组？

这道题的输入有1e6个字符，显然需要$O\left(n\right)$左右级别的算法来解

先看到$num$的定义：不互相重叠的公共前后缀个数

这说明什么？

说明$num$不同于$next$记录的是一个最大值，它记录的是一个和值

而这个和值，是可以推出来的

考虑一个前缀$i$的$next[i]$，它长这样：

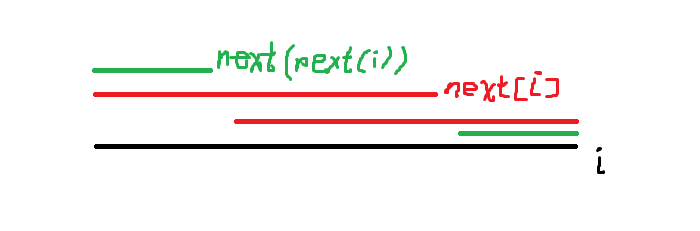
其中，$next[i]$，$next[next[i]]$，$next[next[next[i]]]$......都是这个前缀串i的公共前后缀，而且只有它们是公共前后缀

那么，我们其实只要在求$next$的过程中，顺便把这个公共前后缀的数量递推一下，就得到了一个弱化版的$num$数组：可以重叠的公共前后缀数量，我们称之为$ans$

如何去除有重叠的？

还是看上面那张图

首先$next$数组有一个性质：$next[i] < i$

也就是说，一旦有一个递归了n层的next，比原前缀i的长度的一半要小，那么这个next的递推出的答案$ans$就是i的$num$了

一个问题

假如我们拿到的串是1e6个'a'，那么上面那个算法就会被卡成$O\left(n^2\right)$，道理的话大家可以想一想（每一次递归都只会把next[i]变小1）

那么我们需要做一个优化，来解决这个问题，而解决问题的核心就是：减少重复递归

减少重复递归......有没有想到什么？

没错，就是如同求$next$时一样的方法！

我们将递归用的变量$j$的值不更新，这样，求完了$i$的答案以后，$j$的位置一定在$\frac i2$的左边，也就是它已经满足要求了

这时再递归求解，总时间效率是$O\left(n\right)$的

Code

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
const ll MOD=1e9+7;
int n,fail[1000010],ans[1000010];ll cnt;char a[1000010];
int main(){
    int T,i,j;scanf("%d",&T);
    while(T--){
        scanf("%s",a);n=strlen(a);
        memset(fail,0,sizeof(fail));
        j=0;ans[0]=0;ans[1]=1;
        
        for(i=1;i<n;i++){//求解next
            while(j&&(a[i]!=a[j])) j=fail[j];
            j+=(a[i]==a[j]);fail[i+1]=j;ans[i+1]=ans[j]+1;//递推记录ans
        }
        
        j=0;cnt=1;
        for(i=1;i<n;i++){//求解num
            while(j&&(a[i]!=a[j])) j=fail[j];
            j+=(a[i]==a[j]);
            while((j<<1)>(i+1)) j=fail[j];
            cnt=(cnt*(ll)(ans[j]+1))%MOD;//记得+1
        }
        printf("%lld\n",cnt);
    }
}