自动搬运

查看原文

来自洛谷，原作者为

	hensier **

搬运于2025-08-24 21:36:29，当前版本为作者最后更新于2020-07-03 19:19:00，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

获得更好的阅读体验

这道题有多种解法，我们来逐一分析。

$\color{green}\text{方法1：数组保存法}$

对于输入，我们不仅要输入屏幕，也要保存值为$1$，即白色的位置。我们把白色区域的每一个点都进行保存。

输入以后，我们计算每一个点到所有白点的距离，取其最小并输出。如果该区域已经为白点，即值为$1$，则直接输出$0$即可。

期望得分：$\color{#52C410}100$

时间消耗：$\color{#52C410}354\text{ms}$

程序过程：

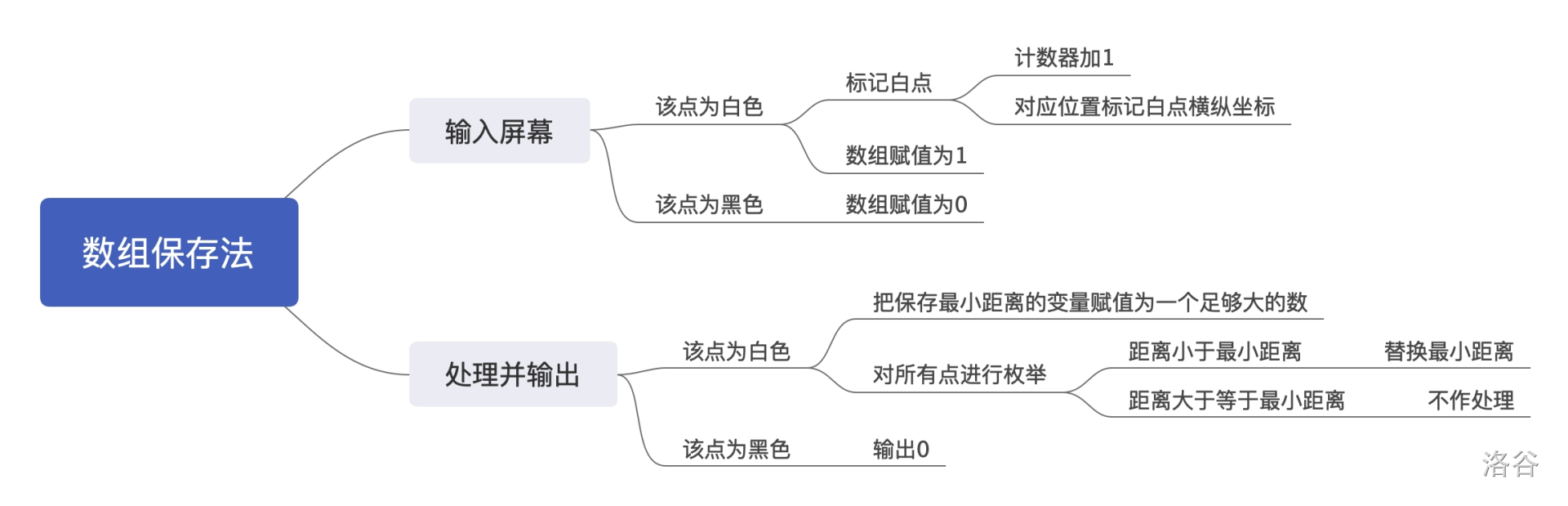
代码解决：

#include<bits/stdc++.h>
#define dist(x_1,x_2,y_1,y_2)abs(x_1-x_2)+abs(y_1-y_2)//定义两点之间的距离公式
using namespace std;
int n,m,white[22501][2],cnt;//white数组保存白点的坐标，cnt保存白点个数
bool screen[151][151];//screen数组保存屏幕，白色为1，黑色为0
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        for(int j=1,x;j<=m;j++)
        {
            scanf("%d",&x);
            screen[i][j]=x;//先给屏幕赋值
            if(x)//如果是白色的就执行
            {
                white[++cnt][0]=i;
                white[cnt][1]=j;
                //点数+1，并且把这个点的坐标进行赋值
            }
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1,dis;j<=m;j++)
        {
            if(screen[i][j])//特判白点可以节省时间
            {
                printf("0 ");//不要漏掉空格
                continue;
            }
            dis=0x3f3f3f3f;//最小距离默认要很大
            for(int k=1;k<=cnt;k++)dis=min(dis,dist(i,white[k][0],j,white[k][1]));//每一次都取最小距离
            printf("%d ",dis);//输出找到的最小距离
        }
        putchar('\n');//换行用putchar更快一些
    }
    return 0;
}

$\color{green}\text{方法2：深度优先搜索}$

这道题用深搜确实不是很合适，但是我们可以通过这题训练我们的搜索能力。

主要的思路就是由每一个黑点开始进行搜索，然后不停地朝$8$个方向拓展并保存最短路径即可。

然而，我们发现，$\text{DFS}$对于解决这种题目来说，实在太慢，效率低下，只有开$\mathcal O2$才能过。

对于搜索（包括深搜和广搜两种方法），拓展的内容如下：

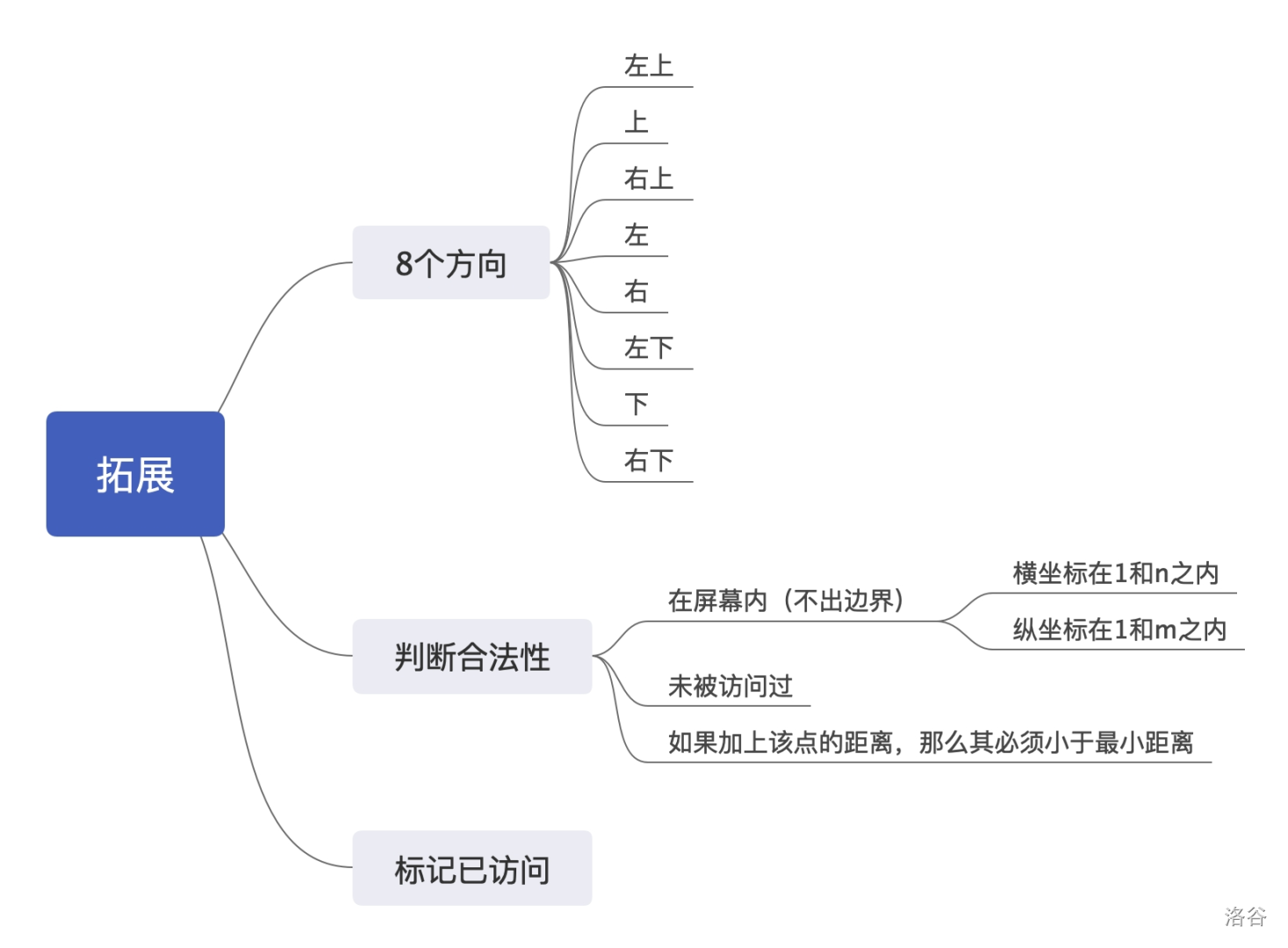
期望得分：$\color{#52C410}90\,\to \,100(\mathcal O2)$

时间消耗：$\color{#FFC116}2.88\text{s}\color{#52C410}\to 1.87\text{s}(\mathcal O2)$

代码实现：

#include<bits/stdc++.h>
#define dist(x_1,x_2,y_1,y_2)abs(x_1-x_2)+abs(y_1-y_2)
using namespace std;
int n,m,dis,dx[]={-1,-1,-1,0,0,1,1,1},dy[]={-1,0,1,-1,1,-1,0,1};//方向增量数组下标有8个
bool screen[151][151],vis[151][151];//screen数组保存屏幕，vis数组保存对应点是否被访问过
void dfs(int x,int y,int d)
{
    if(screen[x][y])dis=d;//如果是白点就更新最小距离
    for(int i=0;i<8;i++)
    {
        int nx=x+dx[i],ny=y+dy[i];//新拓展的点的坐标
        if(nx<1||ny<1||nx>n||ny>m||vis[nx][ny]||d+1>=dis)continue;//如果出了边界、已经被访问或者下一次的距离大于最小距离，就不进行该点的拓展
        vis[nx][ny]=true;//标记访问
        dfs(nx,ny,d+dist(x,nx,y,ny));//新的参数表：横坐标为nx，纵坐标为ny，距离为当前距离加上这两点的距离
        vis[nx][ny]=false;//回溯——标记未访问
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        for(int j=1,x;j<=m;j++)
        {
            scanf("%d",&x);
            screen[i][j]=x;
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            if(screen[i][j])
            {
                printf("0 ");
                continue;
            }
            memset(vis,false,sizeof(vis));//先标记所有点为未访问过
            dis=0x3f3f3f3f;//进行最小距离的初始化
            dfs(i,j,0);//开始搜索，参数表：横纵坐标分别为i和j，初始距离为0
            printf("%d ",dis);//输出最小距离
        }
        putchar('\n');
    }
    return 0;
}

$\color{green}\text{方法3：广度优先搜索}$

$\text{BFS}$的特点是找最优解，所以可以完美地解决本题，而且是这些方法中耗时最少的。

对于搜索（包括深搜和广搜两种方法），大体框架如下：

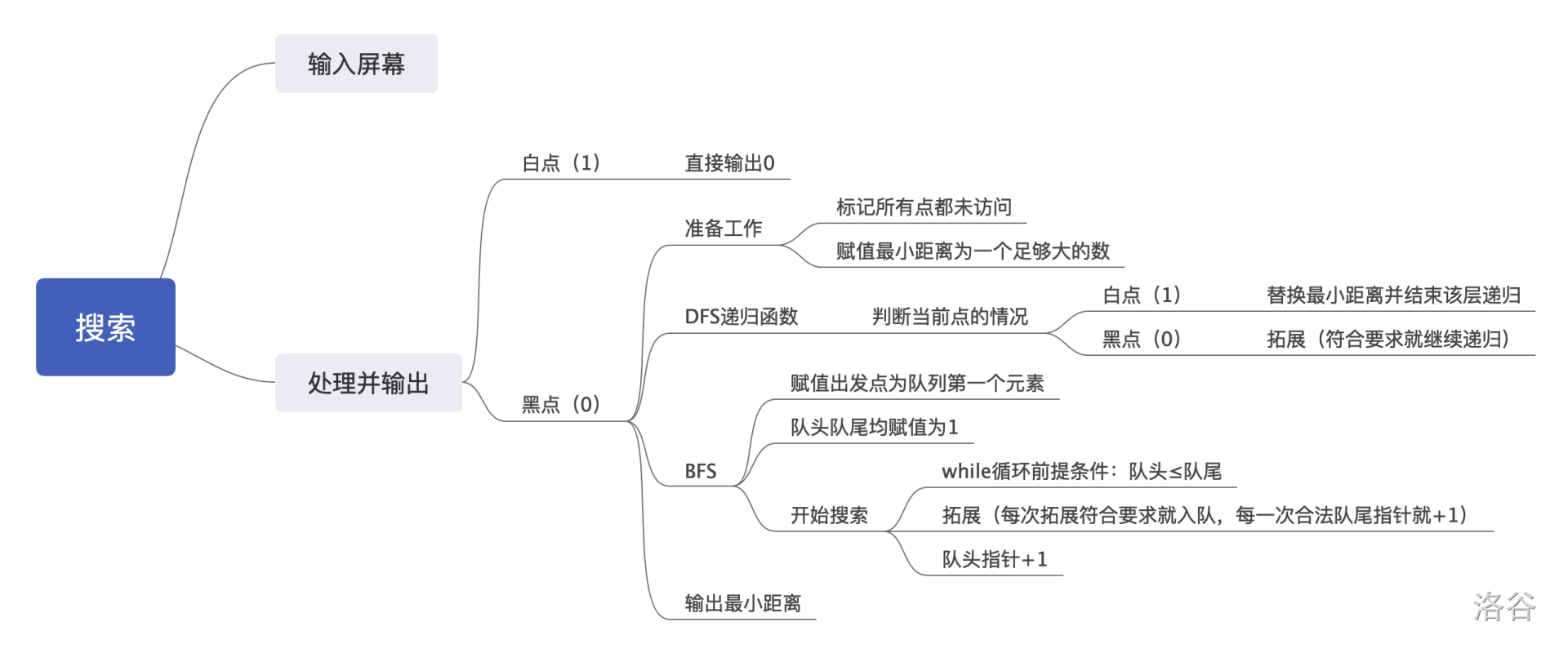
期望得分：$\color{#52C410}100$

时间消耗：$\color{#52C410}73\text{ms}$

代码实现：

#include<bits/stdc++.h>
#define dist(x_1,x_2,y_1,y_2)abs(x_1-x_2)+abs(y_1-y_2)
using namespace std;
int n,m,dx[]={-1,-1,-1,0,0,1,1,1},dy[]={-1,0,1,-1,1,-1,0,1};
bool screen[151][151],vis[151][151];
struct node
{
    int x,y;
}q[22501];//定义结构体类型队列
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        for(int j=1,x;j<=m;j++)
        {
            scanf("%d",&x);
            screen[i][j]=x;
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1,front,rear,dis;j<=m;j++)
        {
            //定义front（队头），rear（队尾）和dis（最小距离）
            if(screen[i][j])//特判
            {
                printf("0 ");
                continue;
            }
            front=rear=1;//一开始队头队尾都为1
            dis=0x3f3f3f3f;
            memset(vis,false,sizeof(vis));//所有元素均为被访问过
            q[1]=(node){i,j};//第一次的状态就是初始位置
            while(front<=rear)
            {
                node f=q[front];
                for(int k=0;k<8;k++)
                {
                    int nx=f.x+dx[k],ny=f.y+dy[k],d=dist(i,nx,j,ny);//保存最小距离
                    if(nx<1||ny<1||nx>n||ny>m||d>=dis||vis[nx][ny])continue;//如果出边界、距离大于等于最小距离或者被访问过就不再继续
                    vis[nx][ny]=true;//标记访问
                    q[++rear]=(node){nx,ny};//入队
                    if(screen[nx][ny])dis=d;//赋值最小距离
                }
                front++;//队头指针加1
            }
            printf("%d ",dis);//输出最小距离
        }
        putchar('\n');
    }
    return 0;
}

总之，虽然一题有多解，但在实际应用中，设法找到最优的方法是至关重要的。