自动搬运

查看原文

来自洛谷，原作者为

	SuperJvRuo **

搬运于2025-08-24 21:36:28，当前版本为作者最后更新于2018-05-05 13:47:20，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

乍一看这题，二分半径，大力simpson啊！看我随手写一个，你看，样例都过了，我交一发......

WA*6+TLE*3+AC*1

半径只能二分解决，而面积，看来不是能用simpson水过的了。

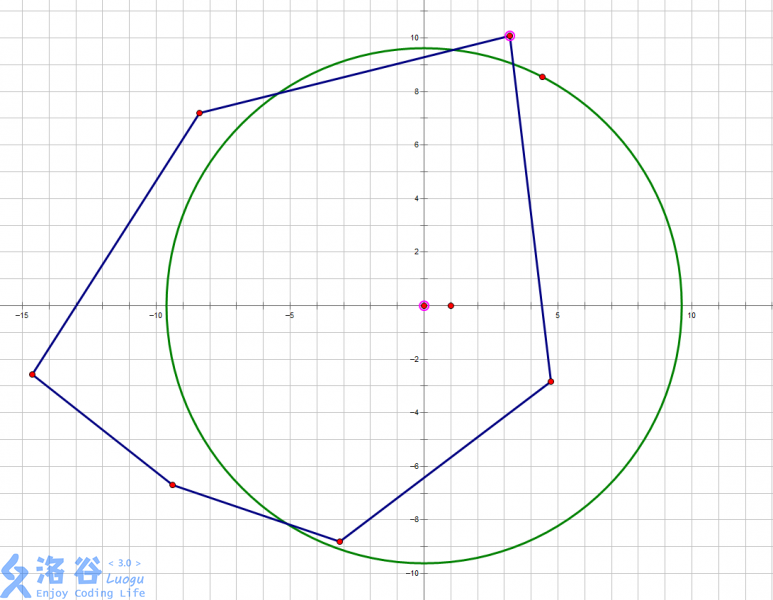
观察图形，利用题中多边形的性质，不难想出这样的搞法：

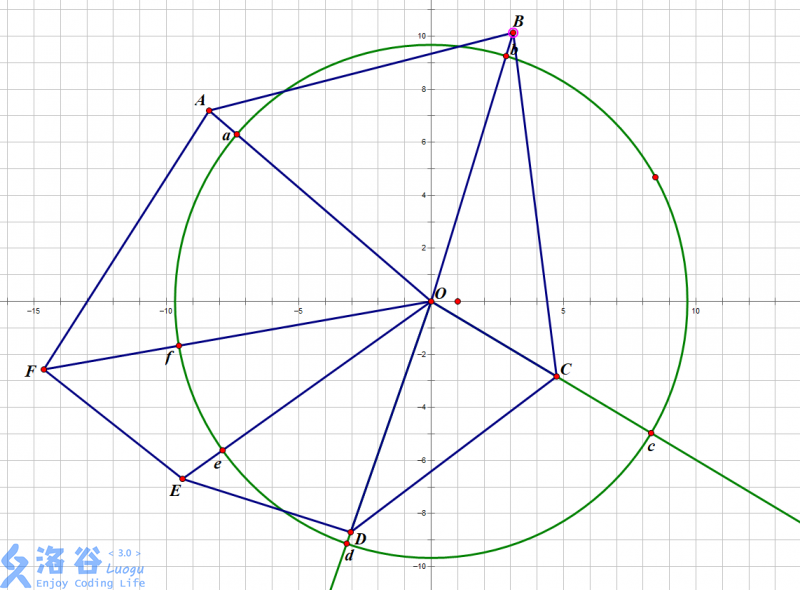
分别连接多边形的各个顶点与原点，将多边形划分为三角形。每个三角形都对应一个唯一的圆心角，在半径确定时，也就能确定一个对应的扇形。只需求出各个三角形与对应扇形面积交的和即可。

这里分为4种情况：

case 1

最简单的情况，如图中$\triangle COD$，三角形被扇形完全包含。那么面积交就是三角形的面积，即：$S=|\vec{OC}\times\vec{OD}|\div2$。

case 2

稍微难一点的情况，如图中$\triangle AOF,\triangle EOF$，三角形完全包含扇形。那么面积交就是扇形的面积，即：$S=r^2\theta\div2$。

关于$\theta$的求法，可以先用坐标分别求出两个点极角的余弦值，再用cmath里的acos函数求出两个极角的弧度。但注意，acos的返回值在$[0,\pi]$间，因此还需要利用点的纵坐标正负，来确定$\theta$是否大于$\pi$，还要用“奇变偶不变，符号看象限”，去确定极角的弧度值。然后两角的极角作差，取绝对值，如果$\theta>\pi$，还要取$2\pi-\theta$。即得$\theta$的弧度。详见下面的代码。

case 3

前两种的结合，如图中$\triangle BOC,\triangle DOE$，角所对的边和弧有且仅有一个交点。可以求出这个交点，然后对交点左右两部分分别用前两种方法求解。那么怎么求交点呢？

设两个点分别为$A(x_1,y_1),B(x_2,y_2)$。设直线$AB$的解析式为$y=kx+b$，则斜率$k=\frac{y_1-y_2}{x_1-x_2}$，纵截距$b=y_1-kx_1$。圆的解析式为$x^2+y^2=r^2$。

由直线解析式得：$$y^2=(kx+b)^2$$

由圆解析式得：$$y^2=r^2-x^2$$

因此有：$$(kx+b)^2=r^2-x^2$$

$$k^2x^2+2kbx+b^2-r^2+x^2=0$$ $$(k^2+1)x^2+2kbx+(b^2-r^2)=0$$

解得：$$x_1=\frac{-2kb+\sqrt{4k^2b^2-4(k^2+1)(b^2-r^2)}}{2k^2+2}$$

$$x_2=\frac{-2kb-\sqrt{4k^2b^2-4(k^2+1)(b^2-r^2)}}{2k^2+2} $$

看看哪个点在线段上就行了。然后一侧求三角形面积，另一侧求扇形面积。

case 4

如果解决了前三种，第四种就不是问题了。如图中$\triangle AOB$，角的对边与对弧有两个交点，可以将其分为两个case 3解决。

是不是很简单啊？

#include<cstdio>
#include<cmath>
#include<algorithm>

#define EPS 1e-5
const double PI=acos(-1);

int n;
double s;
struct Point
{
	double dist,x,y;
} point[55];

//求出线段上离原点最近的点，以确定线段与弧是否相交
Point calc_vertical(Point A,Point B)
{
	Point cross;
    //两种特殊情况：与x轴垂直、与y轴垂直
	if(fabs(A.x-B.x)<EPS)
	{
		cross.x=A.x;
		cross.y=0;
		cross.dist=fabs(A.x);
	}
	else if(fabs(A.y-B.y)<EPS)
	{
		cross.x=0;
		cross.y=A.y;
		cross.dist=fabs(A.y);
	}
	else//作垂线
	{
		double k=(A.y-B.y)/(A.x-B.x);
		double b=A.y-k*A.x;
		cross.x=-b/(k+1.0/k);
		cross.y=-cross.x/k;
		cross.dist=sqrt(cross.x*cross.x+cross.y*cross.y);
	}
    //如果垂足不在线段上，就取两个端点中更近的一个
	if(A.x>B.x)
	{
		std::swap(A,B);
	}
	if(cross.x<A.x||cross.x>B.x)
	{
		cross=A.dist<B.dist?A:B;
	}
	if(A.y>B.y)
	{
		std::swap(A,B);
	}
	if(cross.y<A.y||cross.y>B.y)
	{
		cross=A.dist<B.dist?A:B;
	}
	return cross;
}

//求线段与圆弧的交点
Point calc_cross(Point A,Point B,double radius)
{
	Point res;
	if(A.x>B.x)
	{
		std::swap(A,B);
	}
	double k=(A.y-B.y)/(A.x-B.x);
	double b=A.y-k*A.x;
	res.x=(-2*k*b+sqrt(4*k*k*b*b-4*(b*b-radius*radius)*(k*k+1)))/(2*k*k+2);
	if(res.x<A.x||res.x>B.x)
	{
		res.x=(-2*k*b-sqrt(4*k*k*b*b-4*(b*b-radius*radius)*(k*k+1)))/(2*k*k+2);
	}
	res.y=res.x*k+b;
	res.dist=sqrt(res.x*res.x+res.y*res.y);
	return res;
}

double mult(Point a,Point b)//向量的向量积的模除以2
{
	return fabs(a.x*b.y-b.x*a.y)/2.0;
}

double calc_angle(Point a)//计算极角
{
	double cosine=a.x/a.dist;
	double res=acos(cosine);
	return a.y>0?res:2*PI-res;
}

double calc_sector(Point a,Point b,double radius)//计算扇形面积
{
	double angle=fabs(calc_angle(a)-calc_angle(b));
	angle=angle<PI?angle:2*PI-angle;
	return radius*radius*angle/2.0;
}

double calc_part(Point a,Point b,double radius)//计算面积交
{
	if(a.dist-radius<EPS&&b.dist-radius<EPS)
	{
		return mult(a,b);
	}
	else
	{
		if(a.dist>b.dist)
		{
			std::swap(a,b);
		}
		Point vertical=calc_vertical(a,b);
		if(vertical.dist-radius>EPS)
		{
			return calc_sector(a,b,radius);
		}
		else if(a.dist-radius>EPS)
		{
			return calc_part(a,vertical,radius)+calc_part(vertical,b,radius);
		}
		else
		{
			Point cross=calc_cross(a,b,radius);
			return calc_sector(cross,b,radius)+mult(a,cross);
		}
	}
}

double calc_area(double radius)
{
	double res=0;
	double add;
	for(int i=0; i<n; ++i)
	{
		res+=add=calc_part(point[i],point[i+1],radius);
	}
	return res;
}

int main()
{
	double left_radius=0,right_radius=0,mid_radius;
	scanf("%d %lf",&n,&s);
	for(int i=0; i<n; ++i)
	{
		scanf("%lf %lf",&point[i].x,&point[i].y);
		point[i].dist=sqrt(point[i].x*point[i].x+point[i].y*point[i].y);
		right_radius=std::max(right_radius,point[i].dist);
	}
	point[n]=point[0];

	while(right_radius-left_radius>EPS)//二分半径
	{
		mid_radius=(left_radius+right_radius)/2.0;
		if(calc_area(mid_radius)>s)
		{
			right_radius=mid_radius;
		}
		else
		{
			left_radius=mid_radius;
		}
	}

	printf("%.2lf\n",mid_radius);
	return 0;
}