自动搬运

查看原文

来自洛谷，原作者为

	litble 苟……苟活者在淡红的血色中，会依稀看见微茫的希望（AFO)

搬运于2025-08-24 21:36:09，当前版本为作者最后更新于2018-05-26 17:27:32，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目分析

爱我请戳这里

图挂了请戳这里

老司机

关于老司机的这一部分，显而易见是个dp。将纵坐标相等的点组成的集合称为层，则我们要逐层dp。

将(0,0)这个点看作一棵树，算出答案后再减去它的贡献。

首先预处理出每棵树向左上，上，右上会到哪棵树，这个可以离散+桶完成，正上的处理就是将x坐标放桶里，左上右上的就把经过该点的直线$y=x+b_1$和$y=x-b_2$对应的$b_1$，$b_2$搞进去。

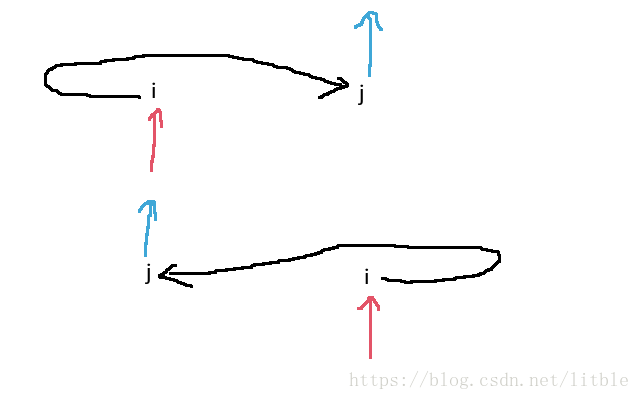
然后就逐层dp撒，如图，会发现假如我们从i点到达该层，从j点离开该层。如果$i<j$，则该层在$j$左边的树都会被走到。如果$i>j$，则该层在$j$右边的树都会被走到。当然啦，如果$i=j$，就只有这棵树会被走到。

我才不会告诉你我一开始没想清楚必须是没许愿的树才能在此转向而GG了一个小时呢

于是我们就可以设$f(i)$表示从i树进入i所在层，可以走的树的最大值。从y最大的层往y最小的处理，对每一层按x排序后，先从左到右扫一遍，再从右往左扫一遍，同时记录一种方案（记录以i进入该层，要以哪个点出去最优和以j出去，是走左上右上还是正上）。

利用我们记录的信息递归输出一种方案，即可获得40分。

小园丁

由于有每层树的个数不超过1000或只有一条路径的限制，所以我们可以从y最小的层往y最大的处理，对于每一个“可以作为这层起点”的树i，枚举这层所有树j，看是否可以从j出去。如果可以，那么j出去达到的树也要标记为“可以作为这层起点”，如此如此，可以弄出所有需要压路机压的路径，但是千万别弄出重边。

这是一个经典的有上下界网络流的模型，即每条边的流量上下界为$[1,inf]$，然后建立源点$S$和汇点$T$，$S$往每个点连一条$[0,inf]$的边，每个点往$T$连一条$[0,inf]$的边。

什么？你不会有上下界网络流？还不去学!就是这篇文章讲的“有源汇最小流”的模型。

可是如果你打完，就TLE了。

以下没看懂文字请直接看代码。

这张图由于比较特殊，所以可以考虑，我们首先让每条边流量等于其下界，那么有些点进出不平衡了嘛，由于$S$和$T$与所有点都有无限流量的边，所以在此时我们可以直接让“积蓄”了流量的点将流量排到$T$，“缺少”流量的点从$S$拿一点来补充，那么此时的流为所有“积蓄”的流量之和。

然后我希望最小流，也就是想让这张图自己“消化调整”，那么求一次超级源汇之间的最大流$kans$，这就是这张图自己不经过S和T做调节的最大限度，“积蓄”流量之和减去$kans$就是答案。

void work2() {
	build();
	S=n+1,T=n+2,ss=n+3,tt=n+4;//呃，其实这个S和T可以删掉
	for(RI i=1;i<=n;++i) {
		if(du[i]>0) adde(ss,i,du[i]),ans+=du[i];//du:如果有[1,inf]边(x,y)，那么++du[y],--du[x]
		else adde(i,tt,-du[i]);
	}
	while(bfs(ss,tt)) ans-=dfs(ss,inf,tt);
	printf("%d\n",ans);
}

代码

哈哈哈哈我没疯放开我我怎么可能敲码农题敲了一下午就疯了呢哈哈哈哈

如果是考场上我肯定选择弃疗。

#include<bits/stdc++.h>
using namespace std;
int read() {
	int q=0,w=1;char ch=' ';
	while(ch!='-'&&(ch<'0'||ch>'9')) ch=getchar();
	if(ch=='-') w=-1,ch=getchar();
	while(ch>='0'&&ch<='9') q=q*10+ch-'0',ch=getchar();
	return q*w;
}
#define RI register int
const int N=50010,inf=0x3f3f3f;
int n,jsx,jsy,js1,js2;
struct node{int x,y,b1,b2,id;}p[N];
int bx[N],by[N],bb1[N],bb2[N];

int up[N],lup[N],rup[N],f[N],Tx[N],Tb1[N],Tb2[N],bj[N],tx[N],ty[N],gup[N],bup[N];
//gup:往上走最多走几棵树，bup:往上走走最多的树，下一步走到哪颗树,bj:记录方案,T开头的都是桶
bool cmpy(node a,node b) {return a.y>b.y;}
bool cmpx(node a,node b) {return a.x<b.x;}
vector<int> iny[N];
void prework() {//预处理每个点左上，右上，正上是那些点
	sort(bx+1,bx+1+n),sort(by+1,by+1+n);
	sort(bb1+1,bb1+1+n),sort(bb2+1,bb2+1+n);
	jsx=1;for(RI i=2;i<=n;++i) if(bx[i]!=bx[jsx]) bx[++jsx]=bx[i];
	jsy=1;for(RI i=2;i<=n;++i) if(by[i]!=by[jsy]) by[++jsy]=by[i];
	js1=1;for(RI i=2;i<=n;++i) if(bb1[i]!=bb1[js1]) bb1[++js1]=bb1[i];
	js2=1;for(RI i=2;i<=n;++i) if(bb2[i]!=bb2[js2]) bb2[++js2]=bb2[i];
	for(RI i=1;i<=n;++i) {
		p[i].x=lower_bound(bx+1,bx+1+jsx,p[i].x)-bx,tx[i]=p[i].x;
		p[i].y=lower_bound(by+1,by+1+jsy,p[i].y)-by,ty[i]=p[i].y;
		p[i].b1=lower_bound(bb1+1,bb1+1+js1,p[i].b1)-bb1;
		p[i].b2=lower_bound(bb2+1,bb2+1+js2,p[i].b2)-bb2;
	}
	sort(p+1,p+1+n,cmpy);
	for(RI i=1;i<=n;++i) {
		int k=p[i].id;
		up[k]=Tx[p[i].x],lup[k]=Tb1[p[i].b1],rup[k]=Tb2[p[i].b2];
		Tx[p[i].x]=Tb1[p[i].b1]=Tb2[p[i].b2]=k;
	}
	sort(p+1,p+1+n,cmpx);
	for(RI i=1;i<=n;++i) iny[p[i].y].push_back(p[i].id);
}
void print(int num) {//输出方案
	int y=ty[num],sz=iny[y].size(),nxt=bj[num];
	if(num!=n) printf("%d ",num);
	if(tx[nxt]<tx[num]) {
		for(RI i=0;i<sz;++i)
			if(tx[iny[y][i]]>tx[num]) printf("%d ",iny[y][i]);
		for(RI i=sz-1;i>=0;--i)
			if(tx[iny[y][i]]<tx[num]&&tx[iny[y][i]]>=tx[nxt]) printf("%d ",iny[y][i]);
	}
	else if(tx[nxt]>tx[num]) {
		for(RI i=sz-1;i>=0;--i)
			if(tx[iny[y][i]]<tx[num]) printf("%d ",iny[y][i]);
		for(RI i=0;i<sz;++i)
			if(tx[iny[y][i]]>tx[num]&&tx[iny[y][i]]<=tx[nxt]) printf("%d ",iny[y][i]);
	}
	if(bup[nxt]) print(bup[nxt]);
}
void work1() {//DP主体
	prework();
	for(RI y=jsy;y>=1;--y) {
		int kmx=0,kbj=0,sz=iny[y].size();
		for(RI i=0;i<sz;++i) {
			int k=iny[y][i];
			if(up[k]&&f[up[k]]>gup[k]) gup[k]=f[up[k]],bup[k]=up[k];
			if(lup[k]&&f[lup[k]]>gup[k]) gup[k]=f[lup[k]],bup[k]=lup[k];
			if(rup[k]&&f[rup[k]]>gup[k]) gup[k]=f[rup[k]],bup[k]=rup[k];
			f[k]=kmx,bj[k]=kbj;
			if(sz-i+gup[k]>kmx) kmx=sz-i+gup[k],kbj=k;
		}
		kmx=kbj=0;
		for(RI i=sz-1;i>=0;--i) {
			int k=iny[y][i];
			if(kmx>f[k]) f[k]=kmx,bj[k]=kbj;
			if(gup[k]+1>f[k]) f[k]=gup[k]+1,bj[k]=k;
			if(i+1+gup[k]>kmx) kmx=i+1+gup[k],kbj=k;
		}
	}
	printf("%d\n",f[n]-1),print(n),puts("");
}

int tot=1,S,T,ss,tt,ans;
int ok[N],du[N],h[N],ne[N*10],to[N*10],flow[N*10],lev[N],q[N];
void adde(int x,int y,int z) {
	to[++tot]=y,ne[tot]=h[x],h[x]=tot,flow[tot]=z;
	to[++tot]=x,ne[tot]=h[y],h[y]=tot,flow[tot]=0;
}
void add(int x,int y) {
	for(RI i=h[x];i;i=ne[i]) if(to[i]==y) return;//注意不要重复（由于数据特殊性不会很慢）
	ok[y]=1,++du[y],--du[x],adde(x,y,inf);
}
void calc(int y,int i) {//暴力查看符合条件的点
	int sz=iny[y].size(),num=iny[y][i];
	for(RI j=0;j<i;++j) {
		int k=iny[y][j];
		if(up[k]&&f[up[k]]+sz-j==f[num]) add(k,up[k]);
		if(lup[k]&&f[lup[k]]+sz-j==f[num]) add(k,lup[k]);
		if(rup[k]&&f[rup[k]]+sz-j==f[num]) add(k,rup[k]);
	}
	for(RI j=i+1;j<sz;++j) {
		int k=iny[y][j];
		if(up[k]&&f[up[k]]+j+1==f[num]) add(k,up[k]);
		if(lup[k]&&f[lup[k]]+j+1==f[num]) add(k,lup[k]);
		if(rup[k]&&f[rup[k]]+j+1==f[num]) add(k,rup[k]);
	}
	if(up[num]&&f[up[num]]+1==f[num]) add(num,up[num]);
	if(lup[num]&&f[lup[num]]+1==f[num]) add(num,lup[num]);
	if(rup[num]&&f[rup[num]]+1==f[num]) add(num,rup[num]);
}
void build() {//网络流建图
	ok[n]=1;
	for(RI y=1;y<=jsy;++y) {
		int sz=iny[y].size();
		for(RI i=0;i<sz;++i) if(ok[iny[y][i]]) calc(y,i);
	}
}
int dfs(int x,int liu,int t) {//dinic的dfs
	if(x==t) return liu;
	int kl,sum=0;
	for(RI i=h[x];i;i=ne[i])
		if(flow[i]>0&&lev[to[i]]==lev[x]+1) {
			kl=dfs(to[i],min(flow[i],liu-sum),t);
			sum+=kl,flow[i]-=kl,flow[i^1]+=kl;
			if(sum==liu) return sum;
		}
	if(!sum) lev[x]=-1;
	return sum;
}
int bfs(int s,int t) {//dinic的bfs
	for(RI i=1;i<=n+4;++i) lev[i]=0;
	int he=1,ta=1; lev[s]=1,q[1]=s;
	while(he<=ta) {
		int x=q[he];++he;
		if(x==t) return 1;
		for(RI i=h[x];i;i=ne[i])
			if(flow[i]>0&&!lev[to[i]])
				lev[to[i]]=lev[x]+1,q[++ta]=to[i];
	}
	return 0;
}
void work2() {
	build();
	S=n+1,T=n+2,ss=n+3,tt=n+4;
	for(RI i=1;i<=n;++i) {
		if(du[i]>0) adde(ss,i,du[i]),ans+=du[i];
		else adde(i,tt,-du[i]);
	}
	while(bfs(ss,tt)) ans-=dfs(ss,inf,tt);
	printf("%d\n",ans);
}

int main()
{
	n=read();
	for(RI i=1;i<=n;++i) {
		bx[i]=p[i].x=read(),by[i]=p[i].y=read();
		bb1[i]=p[i].b1=p[i].y-p[i].x,bb2[i]=p[i].b2=p[i].x+p[i].y;
		p[i].id=i;
	}
	++n,p[n].id=n;
	work1(),work2();
    return 0;
}