自动搬运

查看原文

来自洛谷，原作者为

	BFSBFSBFSBFS **

搬运于2025-08-24 21:36:08，当前版本为作者最后更新于2018-01-20 14:58:20，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

迷宫入口去哪了..

题意.给出1个图.图上有2人.每个人每个回合.可以选择移动到相邻点.或者原地不动.

当2个人相遇就会被....

其中loidc会尽可能延长回合数(就是尽量不相遇.).或者干脆让cony追不上..

而cony会尽力追赶loidc.

由loidc先手.2人均使用最佳策略..求cony能否追上.以及能追上时.至少的回合数.

由于loidc用的最佳策略.显然不会去送..那么对于loidc来讲.就是要求最多的回合数.

---

明确题意后.来看看双方的行动策略.

cony是要追赶loidc的.仔细想想就能明白.cony不会停留在1个点上.

为什么.?

若cony选择在1个点停留.接下来loidc可以继续逃跑.给予了跑掉的可能性.

如果loidc发现逃跑是不行的.Ta依然可以选择停留在原来的点上.相当于先手权仍然在cony这里.但白白浪费了1回合.

不管怎样.停留在1处都不是好方法.所以每回合cony必定移动.

---

这个结论先放在1边.再看看loidc的策略.

如果说要cony追不上的话.loidc唯1的办法是.在被cony抓到之前跑进环.

环至少是3个点吧..2个点的明显是送....

这个好理解吧..在环上1跑1追.速度相同.是追不上的...?

这里有反例了.3角形.

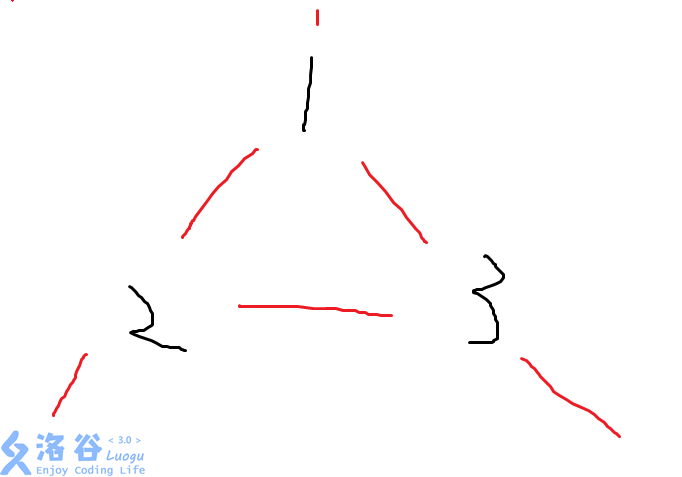
(黑色的是点..红色的是边..丑..).

可以看到,如果loidc在1号点.cony在3号点.即使跑进2号点也无济于事.cony可以马上到达2号点.loidc只能被迫退出3元环..

可是.题目告诉你了没有3角形...那这条就不用管了..

也就是.只要loidc跑进至少4个点组成的环.loidc就不会被抓到.

---

好了.策略分析完毕.那么loidc要怎样跑呢.?

显然.我们要尽快到达环.当然是走最短路了..

但是还有cony啊.不能被捉到.

我们已经知道,cony不会不动.那么让cony也跑最短路.比较1下就行了..

cony难道不能放弃最短路.去拦截在半路loidc.?

既然都能拦截了.那去拦截的这条路+lodic剩下的最短路.又可以组成新的最短路..

也就是不管怎样.cony1定跑在最短路上.

问题就变成了求2点的单元最短路.

设loidc到第i个点的最短路为$d[i]$.cony到第i个点的最短路为$e[i]$.

如果有$d[i] < e[i]$,并且$i$点在有4个点以上组成的环上面.的话.输出NO.

那么跑不进环怎么办.?

只能找个地方躲起来等....

就是说.对于每个$d[i] < e[i]$.输出$max(e[i])$.

就是cony最慢要跑的时间了..

Diu代码..

program P2302;
 uses math;
 type
  wb=array[0..3001] of longint;
  wa=record
   n,t:longint;
  end;
 var
  a:array[0..30001] of wa;
  b,c,h,f,stl,instl,DFS,DFN,t:wb;
  i,m,n,p,dsum,sumstl,ac,bc,upass,smax,x,y:longint;
 procedure hahainc(x,y:longint);    //前向星遍历边..
  begin
   inc(p);
   a[p].n:=h[x];
   a[p].t:=y;
   h[x]:=p;
  end;
 procedure hahaDFS(k,lp:longint);  //用tarjan求环..
  var
   j,p,upass:longint;
  procedure hahaapps;        //初始化工作..
   begin
    inc(dsum);
    DFS[k]:=dsum;           //DFS序.
    DFN[k]:=dsum;           //最靠前访问过的点的DFS序.
    inc(sumstl);            //进栈.
    stl[sumstl]:=k;           //.
    instl[k]:=1;            //是否在栈内的判断..
    f[k]:=1;                //是否访问过的判断..
   end;
  begin
   hahaapps;
   j:=h[k];
   while a[j].n<>-1 do      //遍历边.
    begin
     p:=a[j].t;
     j:=a[j].n;
     if p=lp then continue; //这个是过滤2点环.因为这是无向边..
     if f[p]=0 then
      begin
       hahaDFS(p,k);
       DFN[k]:=min(DFN[k],DFN[p]); //环标记传递.
      end
               else if instl[p]=1 then DFN[k]:=min(DFN[k],DFS[p]); //栈内形成环.
    end;
   if stl[sumstl]=k then upass:=1 //这个是过滤单点环(..)..
                    else upass:=0;
   if DFN[k]=DFS[k] then
    repeat
     p:=stl[sumstl];
     if upass=0 then t[p]:=1;     //t是环标记.
     instl[p]:=0;
     dec(sumstl);
    until p=k;
  end;
 procedure hahadij(var b:wb;k:longint); //做2遍dij..
  var
   i,j,p:longint;
  begin
   filldword(b,length(b),1008208820);
   filldword(f,length(f),0);
   b[k]:=0;
   for i:=1 to n do
    begin
     p:=0;
     for j:=1 to n do
      if (f[j]=0) and (b[j]<b[p]) then p:=j;
     f[p]:=1;
     j:=h[p];
     while a[j].n<>-1 do
      begin
       if b[p]+1<b[a[j].t] then b[a[j].t]:=b[p]+1; //权值是1了..
       j:=a[j].n;
      end;
    end;
  end;
 begin
  readln(n,m,ac,bc);
  filldword(h,length(h),0);
  p:=0;
  for i:=1 to m do
   begin
    readln(x,y);
    hahainc(x,y);
    hahainc(y,x);
   end;
  a[0].n:=-1;
  filldword(f,length(f),0);
  filldword(t,length(t),0);
  filldword(instl,length(instl),0);
  sumstl:=0;
  dsum:=0;
  for i:=1 to n do
   if f[i]=0 then hahaDFS(i,0);
  {for i:=1 to n do
   writeln(DFS[i],' ',DFN[i],' ',t[i]);}
  hahadij(b,ac);
  hahadij(c,bc);
  upass:=0;
  smax:=0;
  for i:=1 to n do
   begin
    if (c[i]>b[i]) and (t[i]=1) then upass:=1;    //能否跑进环的标记.
    if (c[i]>b[i]) then smax:=max(smax,c[i]);     //最长的回合数..
   end;
  if upass=0 then writeln(smax)
             else writeln('NO');
 end.

欢迎Hack.

(ಡωಡ).