自动搬运

查看原文

来自洛谷，原作者为

	TheLostWeak **

搬运于2025-08-24 21:36:00，当前版本为作者最后更新于2019-03-24 23:13:19，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

在博客查看

大致题意： 给定每个点的度数，让你求有多少种符合条件的无根树。

前言：$prufer$序列

简介

$prufer$序列应该是一个比较实用的东西。

据$hl666$大佬说，一切与度数有关的树上计数问题，都可以用它以及它的性质来解决。

而听说$ZJOI$最近特别喜欢出计数题，所以有必要学一学。

转化$1$：从无根树到$prefur$序列

现在，给你一棵树，我们要考虑如何把它变成$prefur$序列。

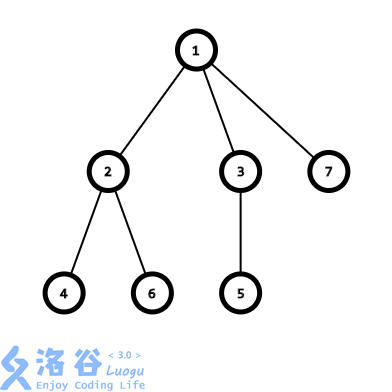
我们需要重复进行以下操作，直至树中只剩下两个点：

• 找到一个度数为$1$，且编号最小的点。（其中编号最小保证了后面将会提到的$prufer$序列的唯一对应性，同时也方便从$prufer$序列转化回无根树）
• 把这个点的父亲节点加入序列，然后把这个点从树中删除。

然后我们就得到了一个长度为$n-2$的序列，这就是$prufer$序列。

所以它有什么实际意义呢？

我也不知道。

以上面的图为例，我们可以模拟这一过程如下：

• 找到$4$号节点，将其父结点加入序列，然后将其删去。此时序列：$\{2\}$。
• 找到$5$号节点，将其父结点加入序列，然后将其删去。此时序列：$\{2,3\}$。
• 找到$3$号节点，将其父结点加入序列，然后将其删去。此时序列：$\{2,3,1\}$。
• 找到$6$号节点，将其父结点加入序列，然后将其删去。此时序列：$\{2,3,1,2\}$。
• 找到$2$号节点，将其父结点加入序列，然后将其删去。此时序列：$\{2,3,1,2,1\}$。

所以，最后得到的$prufer$序列就是$\{2,3,1,2,1\}$。

转化$2$：从$prufer$序列到无根树

还是以刚才那棵树为例吧，我们要考虑如何把它的$prefur$序列变回它本身。

我们需要重复进行以下操作，直至点集中只剩下两个点：（初始化所有点都在点集中）

• 取出$prufer$序列最前面的元素$x$。
• 取出在点集中的、且当前不在$prufer$序列中的最小元素$y$。（这恰好呼应了前面提到过的选取编号最小的节点）
• 在$x,y$之间连接一条边。（注意前面的取出相当于删除）

最后，我们在点集中剩下的两个点中连一条边。

显然这有$n-1$条边，且绝对不会形成环，因此它是一棵树，且就是原树。

以上面的序列为例，我们可以模拟这一过程如下：

• 取出$2,4$连边。此时$prufer$序列：$\{3,1,2,1\}$，点集：$\{1,2,3,5,6,7\}$。
• 取出$3,5$连边。此时$prufer$序列：$\{1,2,1\}$，点集：$\{1,2,3,6,7\}$。
• 取出$1,3$连边。此时$prufer$序列：$\{2,1\}$，点集：$\{1,2,6,7\}$。
• 取出$2,6$连边。此时$prufer$序列：$\{1\}$，点集：$\{1,2,7\}$。
• 取出$1,2$连边。此时$prufer$序列：$\{\}$，点集：$\{1,7\}$。

最后再在$1,7$间连边，就可以得到原树了。

$prufer$序列的性质及相关结论

讲了这么多，我们最关键的还是$prufer$序列的一些性质，以及与其有关的一些结论。（毕竟前面也提到过，我也不知道这东西有什么实际意义）

• 重要性质：$prufer$序列与无根树一一对应。

  这应该显然吧，通过前面的介绍应该可以直接得出。

  而由这个性质，我们才能推导出后面的结论。

• 度数为$d_i$的节点会在$prufer$序列中出现$d_i-1$次。

  当某个节点度数为$1$时，会直接被删掉，否则每少掉一个相邻的节点，它就会在序列中出现$1$次。

  因此共出现$d_i-1$次。

• 一个$n$个节点的完全图的生成树个数为$n^{n-2}$。

  对于一个$n$个点的无根树，它的$prufer$序列长为$n-2$，而每个位置有$n$种可能性，因此可能的$prufer$序列有$n^{n-2}$种。

  又由于$prufer$序列与无根树一一对应，因此生成树个数应与$prufer$序列种树相同，即$n^{n-2}$。

• 对于给定度数为$d_{1\sim n}$的一棵无根树共有$\frac{(n-2)!}{\prod_{i=1}^n(d_i-1)!}$种情况。

  由上面的性质可以知道，度数为$d_i$的节点会在$prufer$序列中出现$d_i-1$次。

  则就是要求出$d_i-1$个$i(1\le i\le n)$的全排列个数。

  而上面那个式子就是可重全排列公式。（即全排列个数除以重复元素内部的全排列个数）

大致就是这些。

解法

现在回到这道题，这显然是一道利用$prufer$序列求解的裸题。

考虑到由$prufer$序列得到的结论：对于给定度数为$d_{1\sim n}$的一棵无根树共有$\frac{(n-2)!}{\prod_{i=1}^n(d_i-1)!}$种情况。

套公式即可。

高精/质因数分解/$Python$

等等，答案小于$10^{17}$？

这看似在$long\ long$范围内，但是我们前面有除法啊！运算过程中肯定会爆$long\ long$！

然后就有$3$种做法：

• 高精。
• 质因数分解。即把每个质因数出现的次数记下来，然后除法就变成了减法。最后相乘即可。
• $Python$！自带高精，写这种题目的必备利器。

我自然是选择了$Python$。

最后提醒一句，需要判无解！

代码

n=(int)(input())#读入n
if n==1:#特判n=1的情况
    x=(int)(input());#读入唯一的节点度数
    if x==0:print(1);#如果这个节点度数为0，说明只有一种解法
    else:print(0);#否则，无解
    exit();#退出程序
f=[0 for i in range(n+5)];f[0]=1;#建立阶乘数组
for i in range(1,n+1):f[i]=f[i-1]*i;#预处理阶乘
ans=f[n-2];tot=0;s=input().split();#初始化ans为(n-2)!，用tot统计度数和来判断是否无解
for i in range(n):
    x=(int)(s[i]);
    if x==0:print(0);exit();#如果存在某个点度数为0，说明图不连通，输出0
    tot+=x-1;ans//=f[x-1];#统计度数和，更新答案
if(tot==n-2):print(ans);#如果度数和为n-2，输出ans
else:print(0);#否则无解