自动搬运

查看原文

来自洛谷，原作者为

	Exber 星铁：152282910 | 博客：https://rebxe.github.io/

搬运于2025-08-24 21:35:59，当前版本为作者最后更新于2021-06-06 11:00:15，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

做法

插头 dp。

这道题其实和模板题是差不多的，只是要开高精度，然后输出的时候 ans 要乘二而已。

首先分析一下题目。很容易发现，一个格子只能经过一次，要不然就不是最短路了。并且一定不会斜着走，因为三角形的两条直角边都比斜边短，“直角边+直角边”一定比“直角边+斜边”短。

注意，在本文里，我把邮筒称作“格子”。

什么是插头 dp？

插头 dp 是一种很神奇的 dp 算法，它还有另外一个大名：轮廓线 dp。顾名思义，轮廓线 dp 就是在一条叫轮廓线的线上进行 dp，而插头 dp 就是在轮廓线的概念上再引入“插头”概念的 dp。

轮廓线是什么?

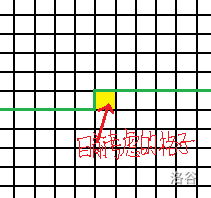
当推到黄色格子时，轮廓线就是那条绿色的线。

而 dp 转移的过程，就像把轮廓线往前推一格，把它从

变成

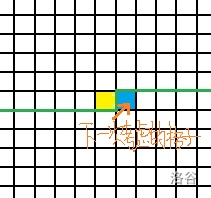
接下来就可以去考虑黄色格子右边的那个格子（蓝色格子）啦。

什么是插头？

插头就像一根链子，把两个格子连了起来。

下图中棕色的就是插头，可以发现它们把格子连了起来

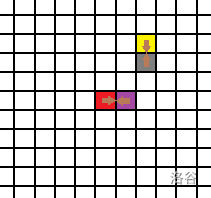
从图中可以发现，每个格子最多能有四个插头，分别指向上、下、左和右。而插头指向的格子必定会有插头指回来，所以插头是成双成对出现的。又因为路径经过格子的话一定有一个插头是进格子的，还有一个是出格子的，所以插头数只能是 2 或者 4。

又由于一个格子只能经过一遍，所以插头数只能为 2。

如何定义状态？

插头 dp 毕竟还是一种 dp，所以还得定义状态。

定义 $dp_{i,j,S}$ 表示递推到格子 $(i,j)$，转移完的轮廓线的状态为 $k$ 时的方案数。

考虑如何表示状态 $k$。

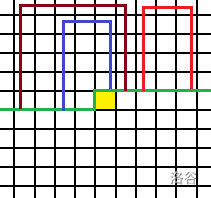
看这张图，很容易发现，轮廓线会把路径切开，每条路径都会先从轮廓线下面穿过轮廓线，转一圈，再从轮廓线上面穿过轮廓线。所以对于每条路径，在轮廓线上都有两个插头，所以所有轮廓线上的插头一一匹配。

但注意，虽然经过轮廓线时方向不同，但插头的方向却都是向下或者向右！

而路径不会相交，要不然就有格子走了两遍了，所以一一匹配的两对插头一定不会相交。

“一一匹配，不会相交”你想到了什么？没错！括号匹配！

括号表示法

可以把一条路径在轮廓线上左边的插头看作左括号 (，把右边的插头看作右括号 )，那么刚才的那幅图就可以变成这样：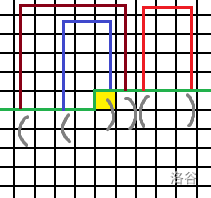

写出来就是:（# 表示没有交点）

(#(##))(#)

看到这里你肯定会感到奇怪，为什么第二和第三个括号之间有两个 #？很简单，因为它们之间有两个插头位置！（一个下插头位置和一个右插头位置）。

到这里，我们终于可以表示状态 $k$ 啦！可以用一个三进制，第 $i$ 位为 0/1/2 时分别表示:

这个位置没有插头/这个位置有一个左括号插头/这个位置有一个右括号插头。

由于三进制实在是太慢太慢了，所以我们采用四进制。

问题又来了，什么插头是左括号插头，什么插头是右括号插头呢？

别急，这个问题在状态转移的时候自然就会解决啦。

如何转移？

首先枚举上一格的状态 $k$。

到这里问题又双叒叕来了：状态实在是太多啦，暴力枚举肯定会 TLE + MLE 的！

所以需要滚动一下数组，只存当前格的信息和上一格的信息，来确保不会 MLE。

对于 TLE，我们可以用哈希表来优化。细心的同学肯定早就发现了，那么多状态里肯定有一大堆不合法的。（括号不匹配）而暴力判断括号匹配麻烦又费事，所以我们采用优秀的哈希技术，把上一格可行的状态全存起来，同时 dp 状态的定义也变成了 $dp_{i,j,k}$ 表示递推到格子 $(i,j)$，转移完的状态编号为 $k$ 时的方案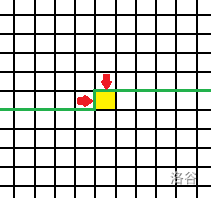数。

由于状态转移只和当前格左边和上面的插头有关系（图中红色的插头），所以定义当前格左边那个往右插的插头状态为 p（0/1/2），当前格上面那个往下插的插头状态为 q（0/1/2）。

终于可以开始分类讨论了。

容易发现，其实一共就只有 7 种状态。

注意，在接下来的状态图中，灰色的箭头表示那里没有插头，红色的箭头表示那里有插头。

1. p==0&&q==0

这时，状态看起来是这样的

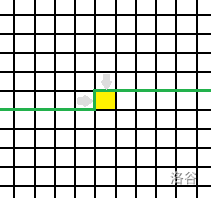
没有插头指向当前格！我们只好新建一个路径了：

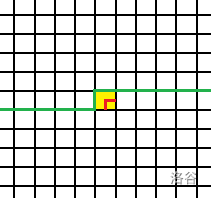
这样，我们就新建了一对括号，解决了之前遗留下来的插头类型问题了。

2. p!=0&&q==0

这时，状态看起来是这样的

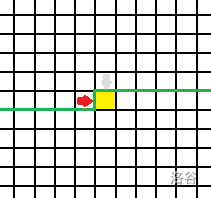
这时，我们可以让它拐个弯儿，或者让它往前走，变成这样

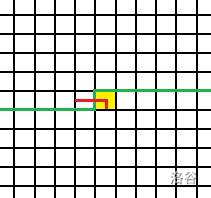
或者这样

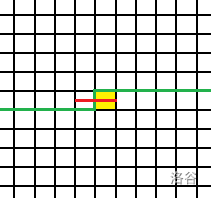
注意，拐弯不能拐去地图边界了，往前走也不能走到地图边界。

p 的类型并不重要，因为转移之后的类型和转移之前的类型相同。

3. p==0&&q!=0

这时，状态看起来是这样的

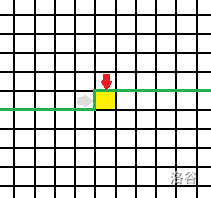
和 2 号状态一样，我们可以让它拐个弯儿或者让它往前走。拐弯也不能拐去地图边界，往前走也不能走到地图边界。

q 的类型依然不重要。

4. p!=0&&q!=0

这时，状态看起来是这样的

对于这种情况，就要分四个子情况讨论了。

• p==1&&q==1

这时，p 和 q 对应的路径是这样的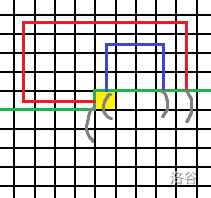

当我们把它们俩连起来后，路径就变成这样了

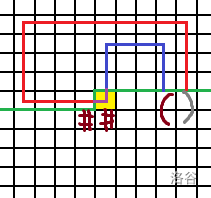
所以我们需要找到 q 对应的右括号（2），把它改成左括号（1），并把 p 和 q 改成井号（0）。

• p==2&&q==2

这时，p 和 q 对应的路径是这样的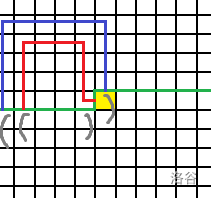

当我们把它们俩连起来后，路径就变成这样了

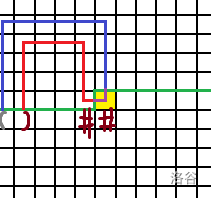
所以我们需要找到 p 对应的左括号（1），把它改成右括号（2），并把 p 和 q 改成井号（0）。

• p==2&&q==1

这时，p 和 q 对应的路径是这样的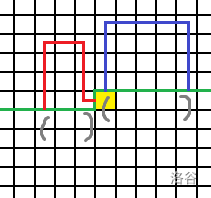

当我们把它们俩连起来后，路径就变成这样了

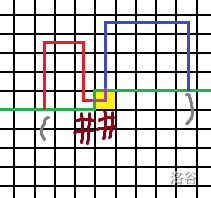
所以我们只要把 p 和 q 改成井号（0）就行了。

• p==1&&q==2

这时，p 和 q 对应的路径是这样的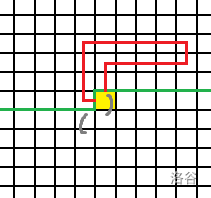

当我们把它们俩连起来后，路径就变成这样了

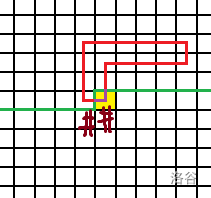
这可不得了！我们把路径闭合起来了！由于轮廓线下面的部分都还没有路径经过，所以这样做只有在 i==n&&j==m 的情况下才是合法的。

合法的话我们只要把 p 和 q 改成井号（0）就行了。

并且闭合之后答案要累加。

如何初始化？

当换行时，我们发现右插头位置没了……

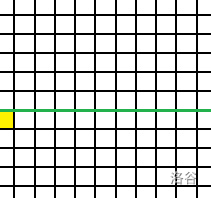
而上一状态却有右插头位置

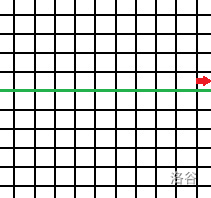
所以要补一个右插头位置。

输出什么？

最后要输出 答案*2。

因为老李可以顺时针走也可以逆时针走。

结束了？

没有……

这题太坑了，并没有 答案对 xxx 取模 这一句话，所以需要高精度……

因为我太懒了，所以高精度直接用了 __int128。（大家千万不要学我，因为 __int128 在赛场上不给用）

最后注意有个特判，当 $n$ 或 $m$ 为 1 时输出 1。

AC 代码

#include <iostream>
#include <cstdio>
#include <cstring>

#define S 300005
#define mod 2001

typedef __int128 ll;

using namespace std;

int n,m;
ll dp[2][S];
int d; // 滚动数组下标 
int tot[2],h[S],nxt[S],val[2][S]; // 哈希表相关 
int only[15]; // only[i] 存 4^i 
ll ans;

void write(ll x)
{
	if(x<0)
	{
		putchar('-');
		x=-x;
	}
	if(x>9)
	{
		write(x/10);	
	}
	putchar(x%10+'0');
}

inline void ins(int x,ll num) // 插入哈希表并更新 
{
	int id=x%mod;
	for(int p=h[id];p;p=nxt[p])
	{
		if(val[d][p]==x)
		{
			dp[d][p]+=num;
			return;
		}
	}
	nxt[++tot[d]]=h[id];
	h[id]=tot[d];
	val[d][tot[d]]=x;
	dp[d][tot[d]]=num;
}

inline void _dp() 
{
	d=0;
	tot[d]=1;
	val[d][1]=0;
	dp[d][1]=1;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=tot[d];j++)
		{
			val[d][j]<<=2; // 初始化：插入一个空插头，补一下右插头位置 
		}
		for(int j=1;j<=m;j++)
		{
			// 滚动 
			int las=d;
			d^=1;
			memset(h,0,sizeof(h));
			tot[d]=0; 
			for(int k=1;k<=tot[las];k++) // 枚举状态 
			{ 
				int zlt=val[las][k]; // 当前状态（zltzlt：zlt 好评） 
				ll num=dp[las][k];
				int p=(zlt>>j*2-2)%4,q=(zlt>>j*2)%4; // 获取 q、p
				// 各种状态 
				if(!p&&!q)
				{
					// 弄一个新路径 
					if(i<n&&j<m)
					{
						ins(zlt+only[j-1]+2*only[j],num);
					}
				}
				else if(p&&!q)
				{
					// 拓展路径 
					if(i<n) // 拐个弯儿 
					{
						ins(zlt,num);
					}
					if(j<m) // 直走 
					{
						ins(zlt+only[j]*p-only[j-1]*p,num);
					}
				}
				else if(!p&&q)
				{
					// 拓展路径 
					if(j<m) // 直走 
					{
						ins(zlt,num);
					}
					if(i<n) // 拐个弯儿 
					{
						ins(zlt-only[j]*q+only[j-1]*q,num);
					}
				}
				else if(p==1&&q==1)
				{
					// 暴力找括号 
					int top=1;
					for(int l=j+1;l<=m;l++)
					{
						if((zlt>>l*2)%4==1)
						{
							top++;
						}
						if((zlt>>l*2)%4==2)
						{
							top--;
						}
						if(top==0)
						{
							ins(zlt-only[j]-only[j-1]-only[l],num); // 改一下 
							break;
						}
					}
				}
				else if(p==2&&q==2)
				{
					// 暴力找括号 
					int top=1;
					for(int l=j-2;l>=0;l--)
					{
						if((zlt>>l*2)%4==1)
						{
							top--;
						}
						if((zlt>>l*2)%4==2)
						{
							top++;
						}
						if(top==0)
						{
							ins(zlt+only[l]-only[j]*2-only[j-1]*2,num); // 改一下 
							break;
						}
					}
				}
				else if(p==2&&q==1)
				{
					ins(zlt-only[j-1]*2-only[j],num); // 连起来 
				}
				else if(p==1&&q==2&&i==n&&j==m)
				{
					ans+=num; // 不得了了！ 
				}
			}
		}
	}
}

int main()
{
	only[0]=1;
	for(int i=1;i<=13;i++) // 初始化 only 数组 
	{
		only[i]=only[i-1]<<2;
	}
	scanf("%d%d",&m,&n);
	if(m==1||n==1) // 特判 
	{
		puts("1");
		return 0;
	}
	_dp();
	write(ans*2); // 记得乘二 
	return 0;
}