自动搬运

查看原文

来自洛谷，原作者为

	Ginger_he .

搬运于2025-08-24 21:35:46，当前版本为作者最后更新于2021-09-11 00:27:57，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目描述

一个 $n\times m$ 的矩阵，求从右下角走到左上角的方案数，每步只能向左或向上走。

引入

逆元

1.什么是逆元？

若有线性同余方程 $ax\equiv1\pmod{b}$，则 $x$ 称为 $a\bmod b$ 的逆元，记作 $x^{-1}$。

2.逆元怎么求？

由逆元的定义有：$ax\equiv1\pmod{b}$
由费马小定理有：$ax\equiv{a^{b-1}}\pmod{b}$
$\therefore x\equiv{a^{b-2}}\pmod{b}$
注意：求逆元还可以用扩展欧几里得法。

3.逆元的基本应用

$x\div y\equiv{x\times y^{-1}\equiv{x\times y^{p-2}\pmod{p}}}$

组合数

1.什么是组合数？

从 $n$ 个不同元素中取出 $m(m\leq n)$ 个元素的所有组合的个数，叫做从 $n$ 个不同元素中取出 $m$ 个元素的组合数。用符号 $\dbinom{n}{m}$ 来表示。

2.组合数如何求？

• 模拟： 按照组合数的定义暴力计算即可，但是这样肯定会爆 long long，最多过 $n\leq12$ 的数据。
• 杨辉三角： 观察下面的图片，若把第 $i$ 行第 $j$ 个数记为 $f(i-1,j-1)$，则 $\dbinom{i}{j}=f(i,j)$，利用这种递推的思想，我们可以过掉 $n\leq100$ 的数据。

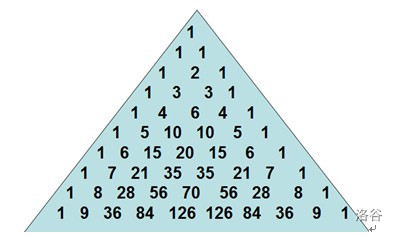
• 逆元求组合数： 运用上述知识，对于一个组合数 $\dbinom{p}{q}=\dfrac{\begin{matrix} \prod_{i=p-q+1}^p i \end{matrix}}{\begin{matrix} \prod_{i=1}^p i \end{matrix}}$，分数线上方的数直接相乘，分数线下方的数都乘其逆元即可。

题解

分析

回归本题，因为每一步只能向左或向上走，所以总步数为 $(1,1)$ 到 $(n,m)$ 的曼哈顿距离，即总的步数为定值 $(n+m)$。接下来考虑从这 $(n+m)$ 步中任意选 $m$ 步向左，根据组合数的定义，答案为 $\dbinom{n+m}{m}$。然后组合数用逆元求值即可。

代码

#include<bits/stdc++.h>
using namespace std;
const long long mod=1e9+7;
long long n,m,ans=1;
long long quickpow(long long a,long long b)//快速幂
{
	long long res=1;
	while(b)
	{
		if(b&1)
			res=res*a%mod;
		b>>=1;
		a=a*a%mod;
	}
	return res;
}
int main()
{
	scanf("%lld%lld",&n,&m);
	for(long long i=n+1;i<=n+m;i++)
		ans=ans*i%mod;//分数线上方直接乘
	for(long long i=2;i<=m;i++)
		ans=ans*quickpow(i,mod-2)%mod;//分数线下方乘逆元
	printf("%lld\n",ans);
	return 0;
}