自动搬运

查看原文

来自洛谷，原作者为

	asuldb 哭晕了喵

搬运于2025-08-24 21:35:34，当前版本为作者最后更新于2018-07-22 08:24:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

$kruskal$重构树，轻松最优解第一

这个东西主要来处理最小生成树的最大边权问题

当然也可以处理最大生成树的最小边权问题

其实这个重构树的核心思想跟 $krsskal$差不多

这张图是样例的最小生成树

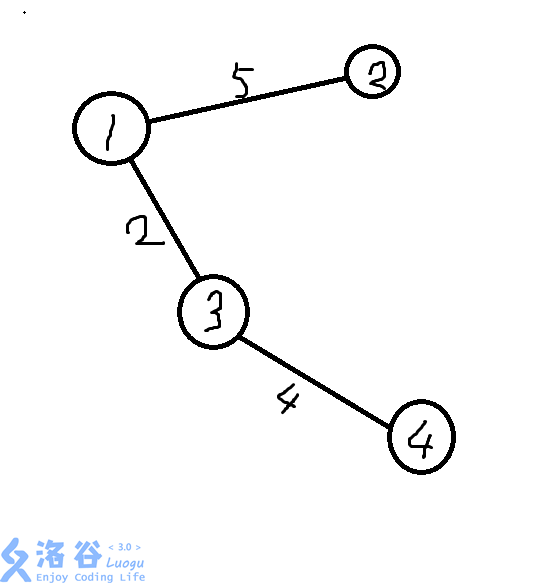
而这张是重构树

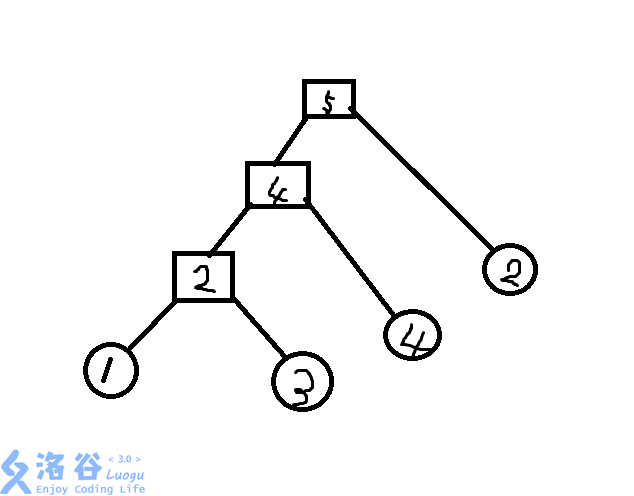
我们看到右图里的重构树中多了一些方点

这些方点是怎么产生的呢

其实这些方点是原来最小生成树里的边

我们重构树的过程是这样的

1. 将所有边按边权从小到大排序

2. 每次最小的一条边，如果条边相连的两个点在同一个集合中，那么就跳过，否则就将这两个点的祖先都连到一个虚点上去，让这个虚点的点权等于这条边的边权

这样的话这课被重构的树就有一些奇妙的性质

1. 原本最小生成树上的点在重构树里都是叶节点

2. 从任何一个点往根上引一条路径，这条路径经过的点的点权单调不降（最大生成树单调不升）

3. 任意两点之间路径的最大边权就是他们的LCA的点权

于是我们重构树之后找一下LCA就行了

这里用的是树剖，还是挺快的

代码

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#define re register
#define maxn 200001
using namespace std;
struct node
{
	int v,nxt,w;
}e[maxn<<2],a[maxn<<2];
int n,m,k,num,Q;
int fa[maxn],top[maxn],f[maxn],deep[maxn],head[maxn];
int sum[maxn],son[maxn],key[maxn];
inline int read()
{
	char c=getchar();
	int x=0;
	while(c<'0'||c>'9') c=getchar();
	while(c>='0'&&c<='9') 
		x=(x<<3)+(x<<1)+c-48,c=getchar();
	return x;
}
inline int find(int x)
{
	if(fa[x]==x) return x;
	return fa[x]=find(fa[x]);
}
inline int add_edge(int x,int y)
{
	e[++num].v=y;
	e[num].nxt=head[x];
	head[x]=num;
}
void dfs1(int r)
{
	sum[r]=1;
	int maxx=-1;
	for(re int i=head[r];i;i=e[i].nxt)
	if(!deep[e[i].v])
	{
		deep[e[i].v]=deep[r]+1;
		f[e[i].v]=r;
		dfs1(e[i].v);
		sum[r]+=sum[e[i].v];
		if(sum[e[i].v]>maxx) maxx=sum[e[i].v],son[r]=e[i].v;
	}
}
void dfs2(int r,int topf)
{
	top[r]=topf;
	if(!son[r]) return;
	dfs2(son[r],topf);
	for(re int i=head[r];i;i=e[i].nxt)
	if(deep[e[i].v]>deep[r]&&son[r]!=e[i].v) dfs2(e[i].v,e[i].v); 
}
inline int LCA(int x,int y)
{
	while(top[x]!=top[y])
	{
		if(deep[top[x]]<deep[top[y]]) swap(x,y);
		x=f[top[x]];
	}
	if(deep[x]<deep[y]) return x;
	return y;
}
inline int cmp(node aa,node bb)
{
	return aa.w<bb.w;
}
int main()
{
	n=read();
	m=read();
	for(re int i=1;i<=m;i++)
	{
		a[i].v=read();
		a[i].nxt=read();
		a[i].w=read();
	}
	sort(a+1,a+m+1,cmp);
	for(re int i=1;i<=(n<<1);i++) fa[i]=i;
	k=n;
	for(re int i=1;i<=m;i++)
	{
		int xx=find(a[i].v);
		int yy=find(a[i].nxt);
		if(xx==yy) continue;
		fa[xx]=fa[yy]=++k;
		add_edge(k,xx);
		add_edge(xx,k);
		add_edge(k,yy);
		add_edge(yy,k);
		key[k]=a[i].w;
	}
	for(re int i=k;i;i--)
	if(!deep[i]) deep[i]=1,dfs1(i),dfs2(i,i);
	Q=read();
	int x,y;
	while(Q--)
	{
		x=read();
		y=read();
		if(find(x)!=find(y)) puts("impossible");
		else printf("%d",key[LCA(x,y)]),putchar(10);
	}
	return 0;
}