自动搬运

查看原文

来自洛谷，原作者为

	原株龙葵 **

搬运于2025-08-24 21:35:31，当前版本为作者最后更新于2019-02-13 11:49:45，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P2241 统计方形

前面几个大佬讲的东西我都看了，数学学得是真好！在此orz了。

但是，题解是给我这种蒟蒻看的，看完了什么也看不懂不就尴尬了吗？

本蒟蒻语数外物化史地政生无一课不弱得要命。

所以，本蒟蒻发得题解一定接地气，保证看懂。

废话不说了，看题解。

首先，统计一个n*m的矩形里有多少个正方形，长方形。

要明确，正方形和长方形都是矩形，那么n*m的矩形里的

矩形数=正方形数+长方形数

明确这一点后，就可以一次求出二者了

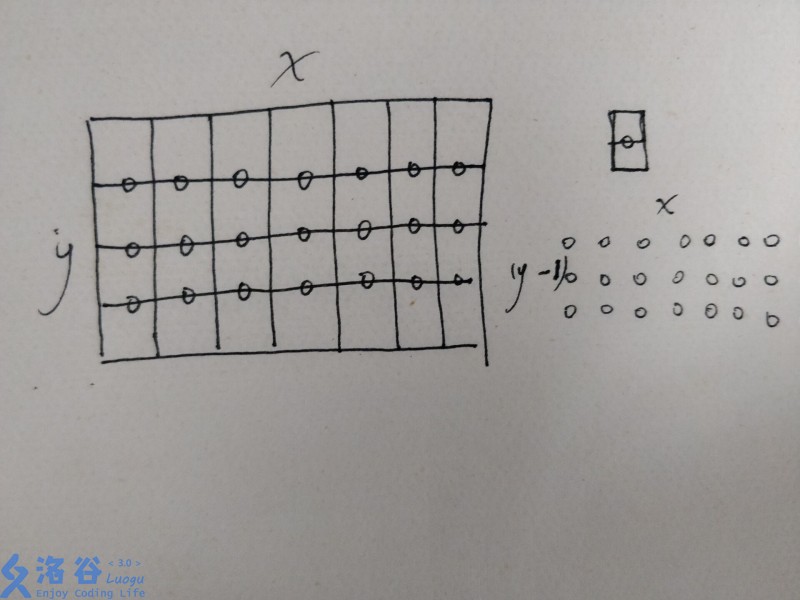
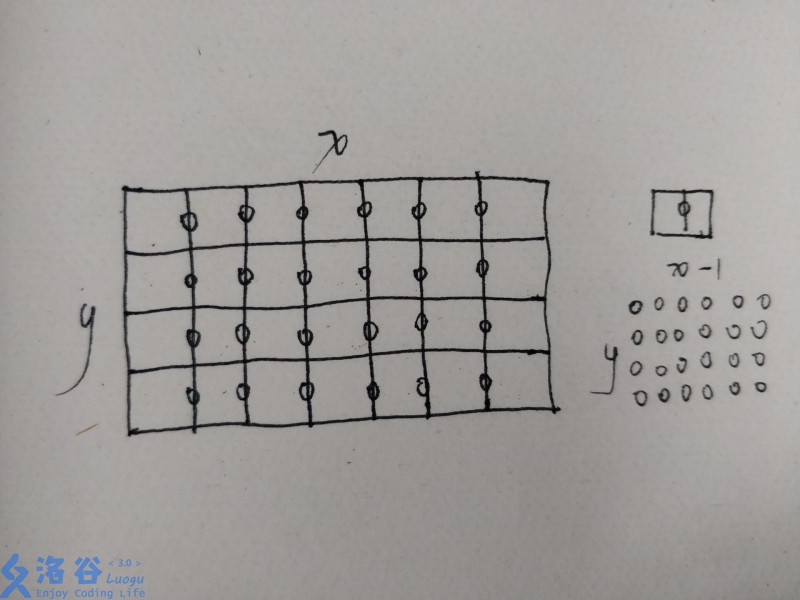
如图，长为2宽为1的小长方形用〇来表示，那么

横向排列的就有 *（n-1）m 个

竖向排列的就有 n（m-1）* 个

证明：

     ∵ 矩形长不等于宽

     ∴ 子矩形构成的矩阵的长宽是由原矩形长宽减去不同数而得
     
     即(n-b)*(m-a) (a≠b)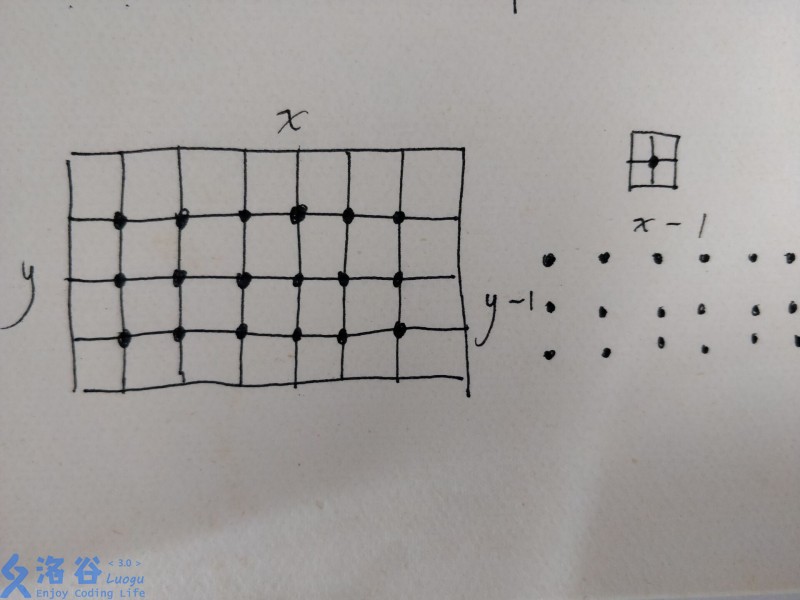

如图，用 · 表示长宽均为二的正方形

即有(n-1)*(m-1)个小正方形

证明：

	∵正方形长等于宽

    ∴子正方形构成的矩阵的长宽由原矩形长宽减去相同数而得
    
    即(n-b)*(m-a) (a=b)

上代码！（最短）

#include<iostream>
using namespace std;
long long n,m,rec,sqr;
int main() {
    cin>>n>>m;
    for(int i=0; i<n; i++)//循环，从n-0到n-(n-1)
        for(int j=0; j<m; j++) {//循环，从m-0到m-(m-1)
            if(i==j) sqr+=(n-i)*(m-j);//如果i==j，说明是正方形
            else rec+=(n-i)*(m-j);//如果不等说明是矩形
        }
    cout<<sqr<<" "<<rec<<endl;//输出
    return 0;
}

本蒟蒻做出普及的题很高兴，代码上的问题还望诸佬多指教。

如果诸佬觉得本蒟蒻的疏才浅学还能略有裨益，勿忘赞

看本蒟蒻这么用心写题解，诸佬真的不点个赞再走吗？^-^