自动搬运

查看原文

来自洛谷，原作者为

	Anguei 俺咕诶

搬运于2025-08-24 21:35:30，当前版本为作者最后更新于2018-01-07 14:21:25，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

为什么没有人推公式呢？我来补充一个。

第一次提交，我打暴力，先构建出一个螺旋矩阵，然后找出指定位置的值。代码大概是这样的：

#include <iostream>

int main() {
    int n, x, y;
    std::cin >> n >> x >> y;
    int a[n][n];
    int tmp = 1;
    for (int i = 0; i < n / 2 + 1; ++i) {
        for(int j = i; j < n - i; ++j)
        	a[i][j]=tmp++;
        for(int j = i + 1; j < n - i; ++j)
        	a[j][n-i-1]=tmp++;
        for(int j = n - i - 2; j > i; --j)
        	a[n-i-1][j]=tmp++;
        for(int j = n - i - 1; j > i; --j)
        	a[j][i]=tmp++;
    }
    std::cout << a[x-1][y-1] << std::endl;
}

但是，只有 $50$ 分，剩下的全都 TLE 了。

由于我太蒻了，想不出来如何在暴力算法上优化，所以换了一种方法——画出矩阵、观察规律、推导公式。

首先，我们画一个 $5 \times 5$ 的螺旋矩阵。

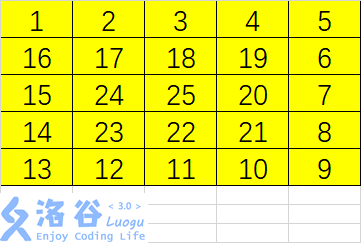
观察一下规律，跟着数字增长的方向走，不难发现：

1. 如果是第 $1$ 行，那么第 $j$ 列的数字就是 $j$；

2. 如果是第 $n$ 列，那么第 $i$ 行的数字就是 $n + i - 1$；

后两条规律有点难找，但是不要放弃，继续观察：

3. 如果是第 $n$ 行，那么第 $j$ 列的数字就是 $3 \times n - 2 - j + 1$；

4. 如果是第 $1$ 列，那么第 $i$ 行的数字就是 $4 \times n - 4 - i + 2$。

好，现在对于每一种情况，我们都推出了一个公式。现在画一个 $6 × 6$ 的螺旋矩阵，验证一下，会发现完全正确：

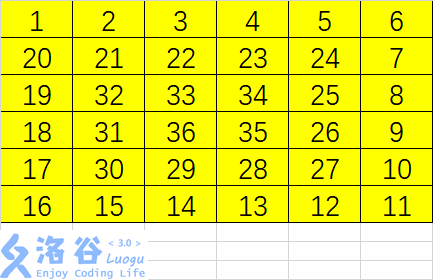
如果对于上述推导过程不是很理解，不妨打开 Excel，自己画图观察。

推导完公式，剩下的就简单多了。不难想出一个递归解法：把螺旋矩阵一层一层地剖开，看看目标位置在哪一层，然后加上这一层最左上角的数字（$4 \times (n - 1)$），即为要求的数字。

于是，递归函数就可以写出来了：

int work(int n, int i, int j) {
    if (i == 1)
    	return j;
    if (j == n)
    	return n + i - 1;
    if (i == n)
    	return 3 * n - 2 - j + 1;
    if (j == 1)
    	return 4 * n - 4 - i + 2;
    // 注意，递归的时候，n 要减 2 而不是减 1
    return work(n - 2, i - 1, j - 1) + 4 * (n - 1);
}

为了避免复制题解的行为，剩下的 main()，留给读者填补。

修了一下 Markdown 和 LaTeX，麻烦管理员重申。