自动搬运

查看原文

来自洛谷，原作者为

	ｃｈｉｌｌ ...

搬运于2025-08-24 21:35:15，当前版本为作者最后更新于2018-03-08 21:58:00，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

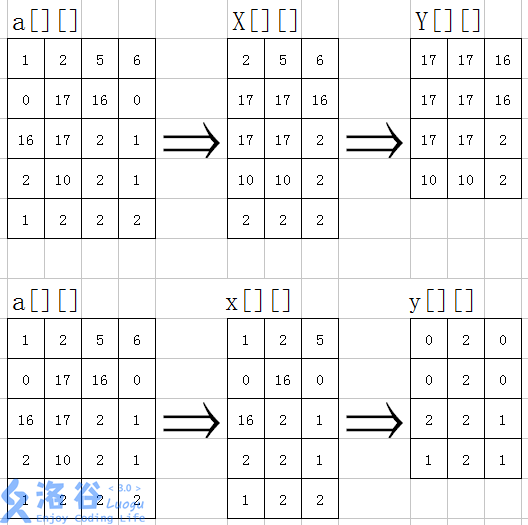
我的思路是...用单调队列分别维护行与列。

具体实现方法:是先用单调队列对每一行的值维护，并将**a[][]每个区间的最大值，最小值分别存在X[][]和x[][]**中。

那么X[][]与x[][]所存储的分别是1×n的长方形内的最大值，最小值。X[i][j]存储第i行第j~j+n-1列的长方形中的最大值。同理，x[i][j]存储第i行第j~j+n-1列的长方形中的最小值。

这时再对这两个数组的每一列上的值进行维护，将X[][]中每个区间的的最大值用Y[][]维护，将x[][]中的每个区间的最小值用y[][]维护。那么Y[i][j]存储X[][]中第i~i+n-1行第j列的长方形的最大值。同理y[i][j]存储x[][]中第i~i+n-1行第j列的长方形的最小值。

故Y[i][j]存储的实为以a[i~i+n-1][j~j+n-1]中的最大，即以i,j为左上角，边长为n的正方形中的最大值。同理，y[i][j]存储的即以i,j为左上角，边长为n的正方形中的最小值。

模拟过程见下图：

附上代码（由于一些习惯，有些变量和题目规定的不太一样。。。）

#include <bits/stdc++.h>
using namespace std;

int n,m,k,front,FRONT,back,BACK,ans;
int a[1001][1001],q[1001],Q[1001];
int x[1001][1001],X[1001][1001];
int y[1001][1001],Y[1001][1001];

int main()
{
	scanf("%d%d%d",&n,&m,&k);
	for (int I=1;I<=n;I++)
		for (int i=1;i<=m;i++)
			scanf("%d",&a[I][i]);
	for (int I=1;I<=n;I++)
		{
			FRONT=BACK=front=back=Q[1]=q[1]=1;
			for (int i=2;i<=m;i++)
				{
					while (a[I][i]>=a[I][Q[BACK]]&&FRONT<=BACK) BACK--;
					while (a[I][i]<=a[I][q[back]]&&front<=back) back--;
					BACK++;back++;Q[BACK]=i;q[back]=i;
					while (i-Q[FRONT]>=k) FRONT++;
					while (i-q[front]>=k) front++;
					if (i>=k) X[I][i-k+1]=a[I][Q[FRONT]],x[I][i-k+1]=a[I][q[front]];
				}
		}
	for (int I=1;I<=m-k+1;I++)
		{
			FRONT=BACK=front=back=Q[1]=q[1]=1;
			for (int i=2;i<=n;i++)
				{
					while (X[i][I]>=X[Q[BACK]][I]&&FRONT<=BACK) BACK--;
					while (x[i][I]<=x[q[back]][I]&&front<=back) back--;
					BACK++;back++;Q[BACK]=i;q[back]=i;
					while (i-Q[FRONT]>=k) FRONT++;
					while (i-q[front]>=k) front++;
					if (i>=k) Y[i-k+1][I]=X[Q[FRONT]][I],y[i-k+1][I]=x[q[front]][I];
				}
		}
    ans=0x3f3f3f3f;
	for (int I=1;I<=n-k+1;I++)
		for (int i=1;i<=m-k+1;i++)
			ans=min(ans,Y[I][i]-y[I][i]);
	printf("%d\n",ans);
	return 0;
}