自动搬运

查看原文

来自洛谷，原作者为

	jins3599 CSP2019RP++

搬运于2025-08-24 21:34:53，当前版本为作者最后更新于2019-11-04 16:54:43，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

非常妙的一道题！

拿到题的第一感觉：带修莫队？？怎么是个蓝题？

然后仔细想了想，其实这道题没有这么困难。

借助于差分的思想，我们考虑区间$[l,r]$的答案是什么。

比如说给定这样一个查询的区间。

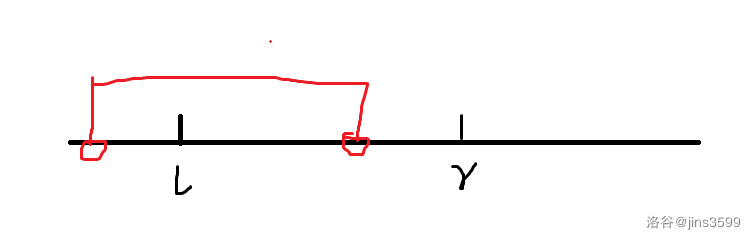
我们首先插入一段红色区间，此时答案数为1。

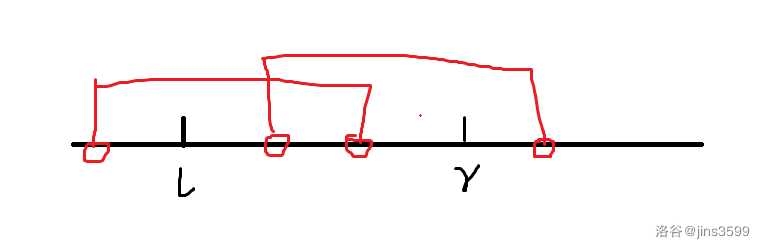
我们再插入一段区间呢？答案数为2.

有什么规律？我们先约定一个区间靠左的端点叫区间的开头，靠右的为区间的结尾。

我们的答案其实就是：

R之前的所有区间开头数（包括R）-L之前的所有区间结尾数（不包括L）

为什么？跨越$[l,r]$的区间一定是区间尾在$[l,r]$内或区间头在$[l,r]$内，或两者都在区间$[l,r]$内。

也就是说我们这样一减，会把所有完全在$[1...l]$区间内的颜色去掉，留下的一定包含在$[l,r]$中。

然后我们只需要维护两个单点修改区间查询的树状数组即可。

#include <bits/stdc++.h>

using namespace std;

int n , m;
const int N = 1e5+ 10;
int t[2][N];//0开头 1结尾 

void add(int x , int pos) {
	while(x <= n) {
		t[pos][x] ++;
		x += x & (-x);
	}
}

int sum (int x , int pos) {
	int ans = 0;
	while(x) {
		ans += t[pos][x];
		x -= x & (-x);
	}
	return ans;
}

int main () {
	scanf("%d %d" , &n, &m);
	while(m --) {
		int opt , l , r;
		scanf("%d %d %d" , &opt , &l , &r);
		if(opt == 1) {
			add(l , 0); add(r , 1);
		} else {
			int rans = sum(r , 0) - sum(l - 1 , 1);
 			printf("%d\n" , rans);
		}
	}
	return 0;
}