自动搬运

查看原文

来自洛谷，原作者为

	caeious 这个家伙很鸽，什么也没留下

搬运于2025-08-24 21:34:31，当前版本为作者最后更新于2018-04-25 17:11:30，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

// 感谢 djq 完善本算法

需要一定思维的一道初等图论题。。。

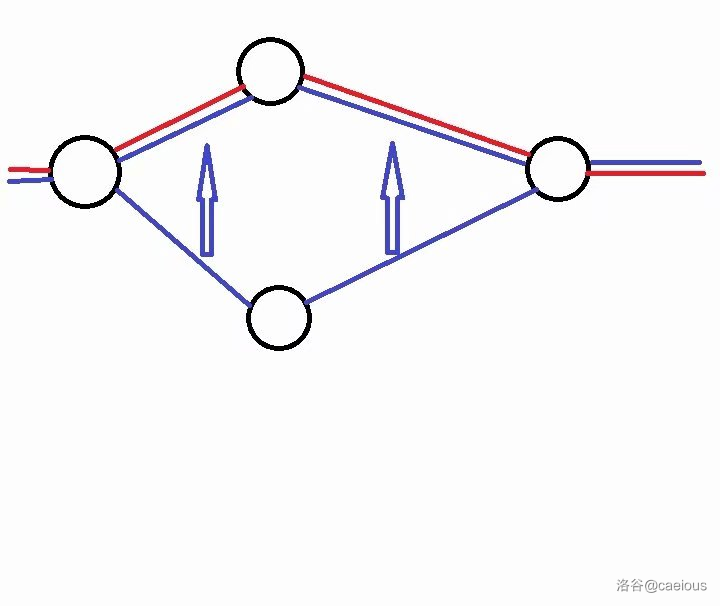
可以证明，所求最长公共路径是一条链，不然由于最短路的一部分还是最短路，而无向图中 $S$ 到 $T$ 与 $T$ 到 $S$ 的最短路相等，可以像下图一样优化：

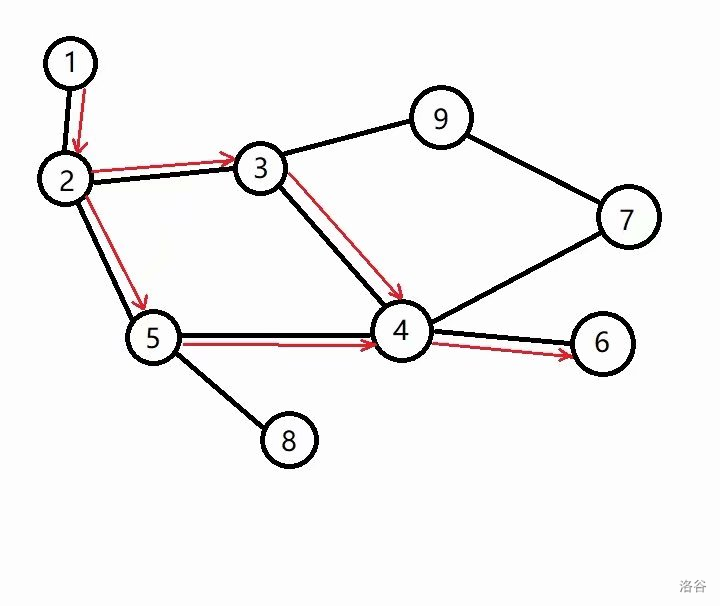
那么我们可以找出 Elaxia 去实验室的最短路经过的有向边组成的 DAG，所求路径一定是该 DAG 上的一条链。样例建成的如下图所示：

同时，所求链也应在 W-- 的最短路 DAG（姑且称为 DAGw）上。如下图：

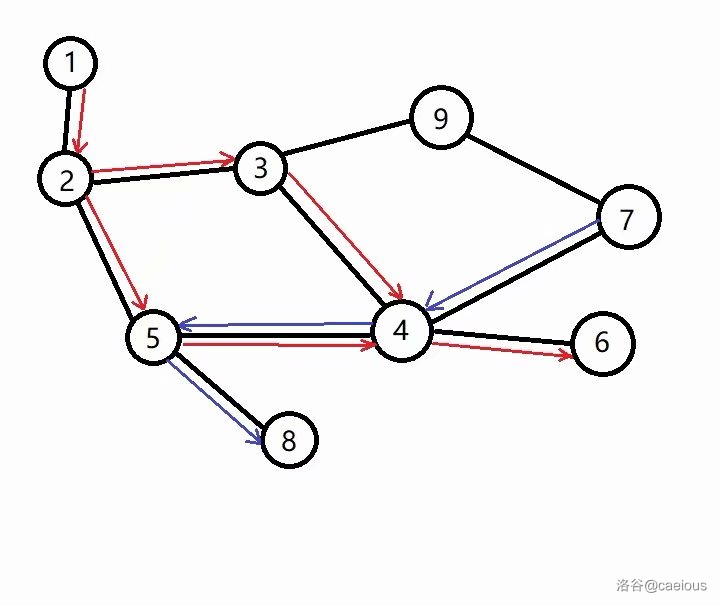
题目说是并行和相遇都算公共，但所求链显然不会又包括并行，又包含相遇，否则因为 DAGw 不可能同时有 $u \to v$ 和 $v \to u$ 边，它在 DAGw 上不是链了。（讨论里的第一组hack数据卡了这一点。）我们可以求一下只保留在两 DAG 中同向出现的边时的最长链，和只保留在两 DAG 中反向出现的边时的最长链。（第二组hack卡了“只保留”三个字）。

参考实现

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<utility>
#include<iostream>
#include<queue>
#include<string>
#define inf 0x3f3f3f3f
#define mp make_pair
#define maxn 1505
using namespace std;
typedef long long ll;
typedef pair<int,int> P;
struct edge{
    int to,cst;
}el[maxn*maxn],el2[maxn*maxn];
int E,n,m,head[maxn],nxt[maxn*maxn],x1,y1,x2,y2,d[5][maxn];
int E2,head2[maxn],nxt2[maxn*maxn],len[maxn],deg[maxn],que[maxn],he,ta;
//变量名带2的都是新建的图的信息。
bool vis[maxn];
inline int getint(){
    char c;
    for(c=getchar();c<'0' || c>'9';c=getchar());
    int res = c - '0';
    for(c=getchar();c>='0'&&c<='9';c=getchar()) res = res * 10 + (c - '0');
    return res;
}
inline void addedge2(int u,int v,int w){
    E2++;
    el2[E2] = (edge){v,w};
    nxt2[E2] = head2[u];
    head2[u] = E2;
    deg[v]++;
}
inline void addedge(int u,int v,int w){
    E++;
    el[E] = (edge){v,w};
    nxt[E] = head[u];
    head[u] = E;
}
inline void dijkstra(int id,int S){
    memset(d[id],0x3f,sizeof(d[id]));
    memset(vis,0,sizeof(vis));
    d[id][S] = 0;
    for(int i=1;i<=n;i++){
        int md = inf,u = -1;
        for(int j=1;j<=n;j++){
            if(!vis[j] && md > d[id][j]){
                md = d[id][j];
                u = j;
            }
        }
        if(u == -1) break;
        vis[u] = true;
        for(int j=head[u];j!=-1;j=nxt[j]){
            d[id][el[j].to] = min(d[id][el[j].to],d[id][u] + el[j].cst);
        }
    }
}
inline void quepush(int x){
    que[ta] = x;
    ta++;
}
inline int quepop(){
    int ret = que[he];
    he++;
    return ret;
}
inline void topo(){
        memset(vis,0,sizeof(vis));
    he = ta = 1;
    for(int i=1;i<=n;i++) if(!deg[i]) quepush(i);
    while(he != ta){
        int u = quepop();
        for(int i=head2[u];i!=-1;i=nxt2[i]){
            deg[el2[i].to]--;
            len[el2[i].to] = max(len[el2[i].to],len[u] + el2[i].cst);
            if(deg[el2[i].to] == 0) quepush(el2[i].to);
        }
    }
}
int main(){
    memset(head,-1,sizeof(head));
    memset(head2,-1,sizeof(head2));
    n = getint();
    m = getint();
    x1=getint(),y1=getint(),x2=getint(),y2=getint();
    for(int i=1;i<=m;i++){
        int u,v,w;
        u=getint(),v=getint(),w=getint();
        addedge(u,v,w);
        addedge(v,u,w);
    }
    dijkstra(1,x1);
    dijkstra(2,y1);
    dijkstra(3,x2);
    dijkstra(4,y2);
    for(int i=1;i<=n;i++){
        for(int j=head[i];j!=-1;j=nxt[j]){
            if(d[1][i] + el[j].cst + d[2][el[j].to] == d[1][y1]){
                if(d[3][i] + el[j].cst + d[4][el[j].to] == d[3][y2])
                addedge2(i,el[j].to,el[j].cst);
            }
        }
    }
    topo();
    int ans = 0;
    for(int i=1;i<=n;i++) ans = max(ans,len[i]);
    memset(head2,-1,sizeof(head2));
    E2 = 0;
    memset(deg,0,sizeof(deg));
    memset(len,0,sizeof(len));
    for(int i=1;i<=n;i++){
        for(int j=head[i];j!=-1;j=nxt[j]){
            if(d[1][i] + el[j].cst + d[2][el[j].to] == d[1][y1]){
                if(d[4][i] + el[j].cst + d[3][el[j].to] == d[3][y2])
                addedge2(i,el[j].to,el[j].cst);
            }
        }
    }
    topo();
    for(int i=1;i<=n;i++) ans = max(ans,len[i]);
    printf("%d\n",ans);
  return 0;
}

附上一组蒟蒻的简单数据：

input：

4 4
1 4 2 3
1 2 10
1 3 1
4 2 9
4 3 2

Output：

2