自动搬运

查看原文

来自洛谷，原作者为

	wangyibo201026 沉舟侧畔千帆过，病树前头万木春

搬运于2025-08-24 21:34:23，当前版本为作者最后更新于2022-06-30 12:19:41，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

思路

首先考虑区间 DP，那么设 $f_{i, j}$ 为颜色块 $i$ 到颜色块 $j$ 全部消完的最大价值。那么转移显然可以这么写：

$$f_{i, j} = \max(f_{i, j}, f_{i, k} + f_{k + 1, j}) $$

此时 $k$ 为枚举的断点，但是显然不够，因为可能出现这种情况：

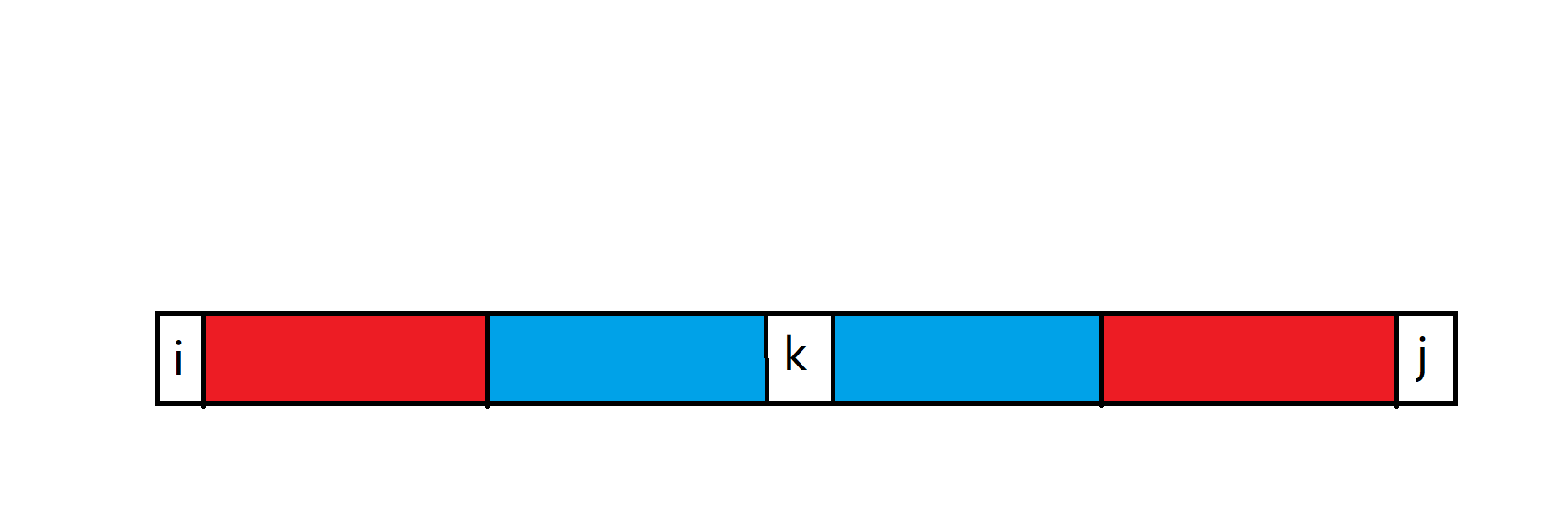
此时明显 $f_{i, k} + f_{k + 1, j}$ 就不是最优的消除方案，因该先把蓝色的全部消掉，再消红色的。

但最大的问题还不是这个，请看图：

此时 $l$ 是在枚举断点时的一个断点，那么最优方案此时就不是 $f_{i, l} + f_{l + 1, j}$，因为明显是要红色的连起来消最优。

很明显，以上情况用两维的 $f$ 都无法解决，所以我们再开一维：

$f_{i, j, k}$ 表示在块 $i$ 到 $j$ 以及后面连续 $k$ 个与块 $j$ 颜色相同的小格最优的消除价值。这里比较抽象，感性理解。

此时又两种转移：

1. 在 $j$ 后面补上 $k$ 位（注意：并非指块）：

$$f_{i, j, k} = \max(f_{i, j, k}, f_{i, j, 0} + (num_j + k) ^ 2) $$

2. $k$ 为 $[i, j]$ 断点，当 $color_k = color_j$ 时，合并 $[i, j]$ 和 $j$ 以及 $j$ 后面 $t$ 位：

$$f_{i, j, t} = \max(f_{i, j, t}, f_{i, k, num_j + t} + f_{k + 1, j - 1, 0}) $$

此时只需预处理出 $suf_i$ 表示 $i$ 色块后面有多少个连续位置的颜色与 $i$ 相同就可以了。

代码

Code：

#include<bits/stdc++.h>

using namespace std;

const int N = 505;

int n;
int color[N], num[N], suf[N], f[N][N][N];

int main(){
    scanf("%d", &n);
    for(int i = 1; i <= n; i++){
        cin >> color[i];
    }
    for(int i = 1; i <= n; i++){
        cin >> num[i];
    }
    for(int i = 1; i <= n; i++){   //预处理出 suf[i]
        for(int j = i + 1; j <= n; j++){
            if(color[i] == color[j]){
                suf[i] += num[j];
            }
        }
    }
    memset(f, 0xcf, sizeof(f));
    for(int i = 1; i <= n; i++){
        for(int j = 0; j <= suf[i]; j++){
            f[i][i][j] = (num[i] + j) * (num[i] + j);   //这里预处理出 f 数组
        }
    }
    for(int len = 2; len <= n; len++){
        for(int i = 1; i + len - 1 <= n; i++){
            int j = i + len - 1;
            for(int k = 0; k <= suf[j]; k++){   //注意：0 也可以
                f[i][j][k] = max(f[i][j][k], f[i][j - 1][0] + (num[j] + k) * (num[j] + k));
            }
            for(int k = i; k <= j - 2; k++){   //这里为什么 j - 1 不行，因为要删掉 k + 1 到 j - 1 的，而 k = j - 1 是无效的
                if(color[k] == color[j]){
                    for(int t = 0; t <= suf[j]; t++){
                        f[i][j][t] = max(f[i][j][t], f[i][k][num[j] + t] + f[k + 1][j - 1][0]);    //这里为什么是 num[j] + t，因为 k 和 j 合并了，所以 j 后面一共有 num[j] + t 个
                    }
                }
            }
        }
    }
    printf("%d\n", f[1][n][0]);
	return 0;
}   

本题真的很难，如果有不理解可以私信。