自动搬运

查看原文

来自洛谷，原作者为

	X_yea 你追逐梦与理想，我带你即刻远航 | 命中注定绽放，何必踟躇彷徨

搬运于2025-08-24 21:34:21，当前版本为作者最后更新于2019-06-30 20:34:53，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

DP解法各位大佬已经说的够详细了

这里就说一下本题的数学解法吧qwq~

数学方法题解

杨氏矩阵

这些就是杨氏矩阵(允许我偷个懒）

我们发现她有如下性质：

• 如果格子(i,j)没有元素，则它右边和下边的相邻格子也一定没有元素。

• 如果格子(i,j)有元素a[i][j]，则它右边和下边的相邻格子要么没有元素，要么有元素且比a[i][j]大。

钩子长度

定义：该格子右边的格子数和它下边的格子数之和。

例如k=3，n=6，每排人数分别为3，2，1时，每个格子的钩子长度如图所示：

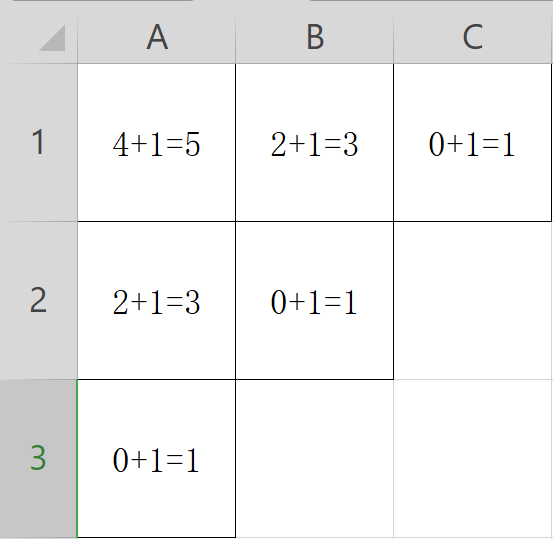
钩子公式

对于给定形状，不同的杨氏矩阵的个数为：n！除以每个格子的钩子长度加1的积。

例如上图的不同的杨氏矩阵的个数=6！/(5 * 3 * 1 * 3 * 1 * 1)=16

CODE

#include <bits/stdc++.h>
#define int long long//记得开long long
using namespace std;

int k,n,a=1,b=1,c,cnt,sum[31],line[6];

int gcd(int a,int b)
{
	return b==0?a:gcd(b,a%b);
}

signed main()
{
	cin>>k;
	for(int i=1; i<=k; i++)
	{
		cin>>line[i];
		n+=line[i];
	}
	for(int i=1; i<=k; i++)
	{
		for(int j=1; j<=line[i]; j++)
		{
			int hook=line[i]-j+1;
			for(int k=i+1; k<=n; k++)
			{
				if(line[k]>=j)
					hook++;
				else break;
			}
			sum[++cnt]=hook;
		}
	}
	for(int i=1; i<=n; i++)//这里是约分，防止溢出
	{
		a*=i;
		b*=sum[i];
		c=gcd(a,b);
		if(c!=1)
		{
			a/=c;
			b/=c;
		}
	}
	cout<<a/b;
	return 0;
}