自动搬运

查看原文

来自洛谷，原作者为

	Hydrogen_Helium 三玖天下第一！！！

搬运于2025-08-24 21:34:17，当前版本为作者最后更新于2019-07-03 14:57:59，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

从题目不难看出这是一道最小生成树的裸题，然后再看数据范围:

$n <= 2300$
$m <= 400000$

首先想到Kruskal或者Prim都可以满足需要，但考虑到这两种算法中Kruskal应用更广，所以今天我们重点讲一下Kruskal算法。

首先回归最小生成树的定义：给定一张边带权的无向图$G = (V, E)$,$n=|V|$,由$V$中$n$个节点和$E$中$n-1$条边构成的无向连通图称为$G$的一棵生成树。边的权值之和最小的生成树被称为最小生成树。

进入今天的正题:Kruskal算法

Kruskal算法是基于一种贪心的思想，他总是维护无向图的最小生成森林。最初，生成森林是由零条边构成，每个节点构成一棵仅包含一个节点的树。

Kruskal算法的主体步骤，就是不断从剩余的边中选出一条权值最小，且他的两个端点在生成森林中分属于两棵不同的树，将这条边加入生成森林中。

那么，我们自然就会想到图的连通性应该如何维护呢？ 为了代码效率和简便，我们一般都采用并查集来维护。（事实上，Kruskal算法的巨大优越性也是在加入并查集优化后才得以体现的，而我们平时所说的Kruskal一般都是带并查集优化的。）

算法流程：

1.建立并查集，每个点构成一个集合。

2.将各边按权值从小到大排序，依次扫描每条边。

3.若一条边两端点在同一集合中，则忽略这条边直接跳过。

4.否则，合并他们所在的集合，将权值之和累加到答案中。

5.第四步中选中的边就构成了这张图的最小生成树。

一图胜千言：

这是一幅无向图：

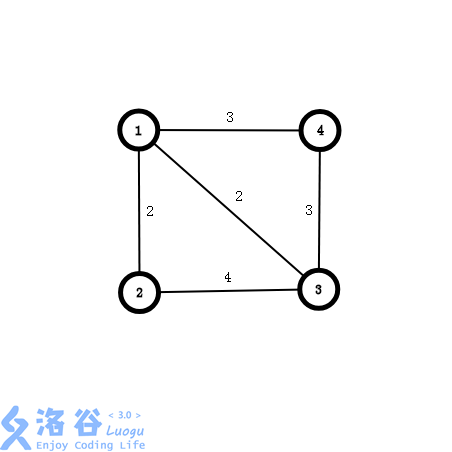
将各边按权值从小到大排完序后应为：

x      y       val
1      2        2
1      3        2
1      4        3
3      4        3
2      3        4

然后我们开始执行Kruskal的主体流程：

枚举第一条边（1, 2, 2），将其加入生成森林中，生成森林变为：

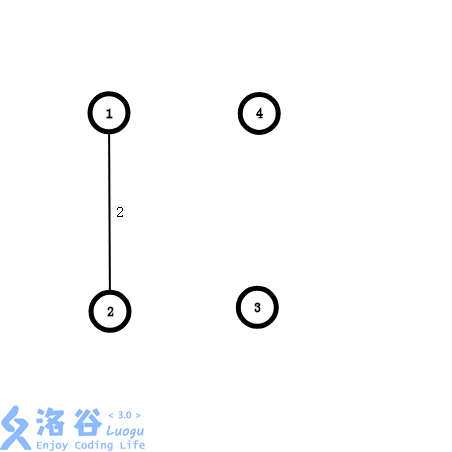
枚举第二条边（1, 3, 2），将其加入生成森林中，生成森林变为：

枚举第三条边（3，4，3），将其加入生成森林中，生成森林变为：

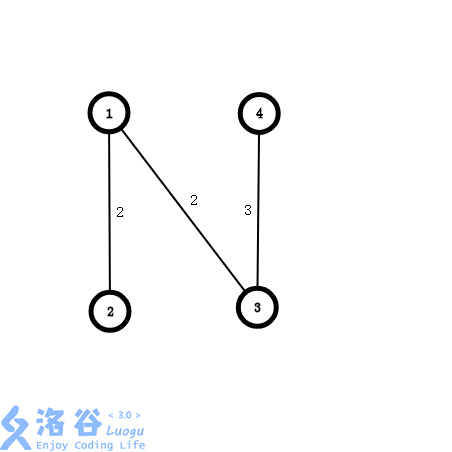
你会发现，此时我们已经选出$n - 1$条边，那么这就是这张图的最小生成树，将权值累加起来即为答案，Kruskal算法结束。

Ps：这幅图比较简单，但是重在理解Kruskal的流程。

原理理解之后，代码就会变得异常简单了，注意，重点在于一定要理解，废话不多说，直接上代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define maxn 400005

using namespace std;

int n, m, fa[maxn], tot, head[maxn], sum;

struct Edge{
	int x, y, w;
}edge[maxn];

bool cmp(Edge x,Edge y){return x.w < y.w;} //自定义比较函数

int find(int x){reutnr x == fa[x] ? x : fa[x] = find(fa[x]);}

bool judge(int x,int y){return find(x) == find(y);}

void merge(int x,int y){fa[find(x)]=find(y);}
//优雅的三行并查集
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= m; i++){
		cin >> edge[i].x >> edge[i].y >> edge[i].w;
		edge[i].x++, edge[i].y++;
	}
	sort(edge+1, edge+m+1, cmp); //权值从大到小排序
	for(int i = 1; i <= n; i++) fa[i] = i;
	for(int i = 1; i <= m; i++){
		int x = edge[i].x, y = edge[i].y;
		if (!judge(x,y)){
            sum += edge[i].w;
			merge(x,y);
		}
	}                           //当然，这部分也可以封装到函数中，看个人喜好
	cout << sum << '\n';
	return 0;
}

最后，本篇题解旨在帮助那些刚刚接触到最小生成树的OIer们更好的理解，若有任何问题，请私信本人。