自动搬运

查看原文

来自洛谷，原作者为

	keep_ El Psy Congroo

搬运于2025-08-24 21:34:00，当前版本为作者最后更新于2020-11-21 21:44:36，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P2101 命运石之门的选择 （分治)

介绍

El Psy Congroo

题目链接

没错，作为石头门厨，怎么能不做石头门的题呢？(在搜石头门的时

候搜到了本题)

本题作为一道分治基础练习题还是不错的，虽然看起来挺简单,但还

是有不少需要思考的地方的。(可能是我太菜了)

分析

我们对本题进行分析，

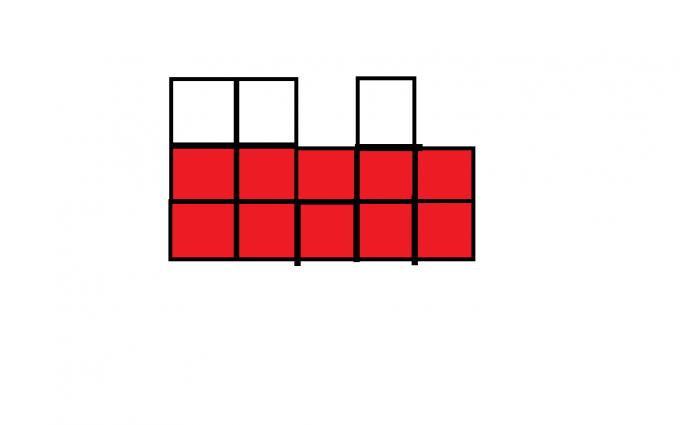
就拿下面这个图举例

我们首先观察到了红色部分，红色部分是当前所能构成的最大矩形

我们拥有两种涂色方法，横着涂和竖着图，因为涂一次色的代价与涂

色面积无关，所以我们每一次涂色需要尽可能的多涂。

对于红色部分，显然，全部采用同一种涂色方法是要比两

种方法同时采取更优的，因为当我们混用涂色方法时，一定是可以

通过去掉某一次涂色来降低所需代价的。

针对红色部分，如果我们全部采用竖着涂，因为我们要尽可能的多

涂，所以我们既然可以竖着涂完红色部分，也可以在同代价下涂完

整个图，所以我们目前涂完整个图的代价就是当前图形的宽度，如

果我们采用横着图，涂完整张的总代价就是（该图形中最低的小矩

形的高度）+（涂完红色部分以外部分的最小代价）

我们所要求的答案就是这两种方法的代价最小值

那如何求出涂完红色部分以外部分的最小代价呢？

这时候就要采用分治思想了，

我们用原图形减去红色部分，得到了一个或几个图形，我们目前要

求的就是涂完所有新图形的最小代价，我们针对每一个新图形都按

先前求原图形的最小代价的方法处理，最后将其合并即可。

放一下代码

#include<cstdio>
#include<cstring>
#include<string>
#include<iostream>
#define int long long
using namespace std;
const int maxn=1e4;
inline int read(){
	int ret=0;
	int f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-')	
			f=-f;
		ch=getchar();
	}
	while(ch<='9'&&ch>='0'){
		ret=ret*10+(ch^'0');
		ch=getchar();
	}
	return ret*f;
}
int n;
int m;
int a[maxn];
int slove(int l,int r){
	if(l==r){
		return 1;//边界
	}
	int t=r-l+1;//目前图形的宽度
	int minn=0x3f3f3f3f;
	for(int i=l;i<=r;i++){
		if(a[i]<minn){
			minn=a[i];//找到最低矩形的高度
		}
	}
	int ans=minn;
	for(int i=l;i<=r;i++){
		a[i]-=minn;//减掉红色部分
	}
	int ll=l;
	for(int i=l;i<=r;i++){
		if(a[i]&&!a[i-1])
			ll=i;
		if(a[i]&&(!a[i+1]||i==r)){
			ans+=slove(ll,i);//分治处理
		}
	}
	return min(ans,t);
}
signed main(){
//	freopen("a.txt","r",stdin);
	n=read(); 
	for(int i=1;i<=n;i++){
		a[i]=read();
	}
	cout<<slove(1,n); 
	return 0;
} 

这一切都是命运石之门的选择