自动搬运

查看原文

来自洛谷，原作者为

	emptysetvvvv 这里埋葬着一位 OIer 的青春

搬运于2025-08-24 21:33:47，当前版本为作者最后更新于2019-02-02 18:24:54，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

背景

Update2022.2.22: 纪念我的首篇题解，虽然我已经是个失败者了，但是 zcysky 成我班助了！有空更张 zcysky 照片（逃

思路

PART I

题意：给定带权的树或基环树，从随机一点出发走每个点至多经过一次的路径，问期望路径长度。

$son_u$ 表示 $u$ 的子结点数量；$fa_u$ 表示 $u$ 的父结点数量，取值为 $1$ 或 $2$（因为有环）。

$down_u$ 表示从 $u$ 出发，第一步向下走的期望路径长度，「下」指子结点方向即叶子方向；

$up_u$ 表示从 $u$ 出发，第一步向上走的期望路径长度，「上」指父结点方向。

注意：只规定了第一步向上走，第二步允许去 $u$ 的父亲 $k$ 的其他子结点。

那么从 $u$ 出发的期望路径长度为：

$$\large ans_u=\dfrac{down_u\cdot son_u+up_u\cdot fa_u}{son_u+fa_u} $$

PART II

先考虑 50pts 的普通树做法。

$down_u$ 显然只不依赖任何的 $up$ 值：

$$\large down_u=\dfrac{1}{son_u}\sum_{v\text{ is son of }u}(down_v+w_{u,v}) $$

$v$ 是 $u$ 的子结点，$w_{u,v}$ 表示边权。特别的，叶子结点 $down$ 值为 $0$。

对于普通树，$u$ 至多有一个父结点 $k$，而 $up_u$ 是要依赖 $up_k,down_k$ 的：

$$\large up_u=w_{u,k}+\dfrac{up_k\cdot fa_k+down_k\cdot son_k-down_u-w_{u,k}}{fa_k+son_k-1} $$

解释如下：

不论如何，第一步贡献 $w_{u,k}$。

粗略地看，继续向上走贡献 $up_k\cdot fa_k$，转而向下走贡献 $down_k\cdot son_k$，考虑到不能走回来，故应减去 $down_u+w_{u,k}$。

第二步向上有 $fa_k$ 种选择，向下有 $son_k-1$ 种选择（不允许回来），故分母为 $fa_k+son_k-1$。

特别的，若 $k$ 仅与 $u$ 相连即 $fa_k+son_k-1=0$，则 $up_u=w_{u,k}$，没有后一项。

实现时，计算 $up,down$ 值，由于前者依赖后者，而后者不依赖前者，故流程如下：

1. 从根节点开始，递归每个子结点计算 $down$ 值；
2. 递归至 $u$ 时，先递归子结点，得到每个 $down_v$，然后计算 $down_u$，返回；
3. 得到该普通树的 $down$ 值后，从根节点的每个子结点开始，递归计算 $up$ 值；
4. 递归至 $u$ 时，根据父结点 $k$ 的信息计算 $up_u$，然后递归子结点计算，返回；
5. 根据 $up_i,down_i$ 计算 $ans_i$，最终结果为 $\displaystyle\dfrac{1}{n}\sum_{i=1}^nans_i$。

PART III

再来考虑基环树的情况。

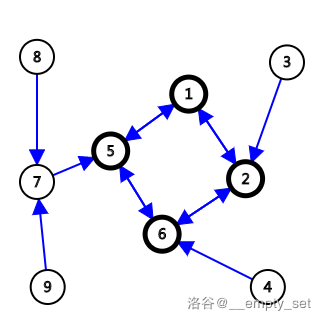
如图所示是一棵并不优美的基环树，箭头指向父结点（$1$ 或 $2$ 个），加粗结点是环上结点，以下简称「黑点」，其余结点简称「白点」。

我们将基环树看做若干普通树根节点相连成环的结果。

注意到无论从哪一点出发，第一步向下，活动范围始终在普通树内部，即：无论黑白，$down$ 值不变。

若 $u$ 是白点，只有唯一父亲 $k$，尽管此时 $fa_k$ 不一定为 $1$（白点 $u$ 的父亲 $k$ 是黑点时 $fa_k=2$），但显然考虑推导过程，$up_u$ 仍符合上文的公式。

若 $u$ 是黑点，则 $up_u$ 的计算显得和繁琐。

$u$ 第一步去了另一个黑点，第二步可以选择继续在环上走，还可以选择钻入该黑点的子树。

为了方便处理，我们先通过深搜得到：

• 黑点总数 $t$；
• $\text{dfn[u]}$，维护 $u$ 是搜到的第几个黑点；
• $\text{path[i]}$，维护第 $i(1\leqslant i\leqslant t)$ 个黑点的实际编号 $u(1\leqslant u\leqslant n)$；
• $\text{disl[i],disr[i]}$，类似于链表的意味，维护第 $i$ 个黑点与左右相邻黑点的距离。

对于黑点 $u$，先规定第一步必须逆时针走，则有：

$$\large up_u=\sum_{i}P_i\times \left(\dfrac{down_{\text{path[i]}}\cdot son_{\text{path[i]}}}{son_{\text{path[i]}}+1}+w\right) $$

其中，$i$ 依次取 $\text{dfn[u]}+1,\text{dfn[u]}+2,\text{dfn[u]}+3,\ldots,t,1,2,3,\ldots\text{dfn[u]}-1$。

嗯，这个式子有失数学美感，但严谨的讲，的确是这个样子。不要紧，我们来看看这是什么意思。

根据期望的定义，期望等于执行第 $k$ 步的概率与第 $k$ 步带来的贡献的乘积的累加和。

先来看概率，$P_i$ 表示走到该点的概率，规定了第一步逆时针，即 $P_{\text{dfn[u]}+1}=1$。

第 $i$ 个黑点的下一个黑点是 $i\bmod t+1$，需要在第 $i$ 个黑点的 $son_{\text{path[i]}}$ 个子结点和下一个黑点之中选择下一步去哪里，那么 $P_{i\bmod t+1}=\dfrac{1}{son_{\text{path[i]}}+1}P_i$。

再来看从顺时针方向的上一个黑点走到第 $i$ 个黑点的贡献，首先有边权 $w$，即 $\text{disl[i]}$。

其次，我们需要考虑如果从此钻入第 $i$ 个黑点的子树产生的贡献，即 $\dfrac{down_{\text{path[i]}}\cdot son_{\text{path[i]}}}{son_{\text{path[i]}}+1}$。

特别的，如果第 $i$ 个黑点逆时针方向的下一个黑点就是 $u$ 的话，只能选择钻入子树而不能继续走重复的，那么分母就应该为 $son_{\text{path[i]}}$ 即钻入该子树的贡献直接就是 $down_{\text{path[i]}}$。

刚刚规定了第一步必须逆时针走，现在再规定第一步必须顺时针求一遍，最终给 $up$ 值除以 $2$ 即可。

当然，也可以在一开始就令 $P=\dfrac{1}{2}$，代码中也是这样实现的。

这很好理解，由于路径不重复，所以不可能顺逆时针交替，顺逆各求一遍一定包含了所有情况，只不过每个概率都放大了 $2$ 倍，现在除以 $2$ 即可。

理清逻辑关系，所有 $down$ 值只依赖其子结点的 $down$ 值，黑点的 $up$ 值依赖 $down$ 值，白点的 $up$ 值依赖黑点的 $up$ 值和 $down$ 值，故流程如下：

1. 从每个黑点即每个普通树的根节点开始，递归每个子结点计算 $down$ 值，方法同普通树；
2. 计算每个黑点的 $up$ 值，顺逆时针各求一遍，然后除以 $2$，如上文所示；
3. 从每个黑点的每个子结点开始，递归计算白点的 $up$ 值，方法同普通树；
4. 根据 $up_i,down_i$ 计算 $ans_i$，最终结果为 $\displaystyle\dfrac{1}{n}\sum_{i=1}^nans_i$。

代码

带空格有注释，神犇请自行跳过。

实际上， $\varnothing$ 是一个蒻不禁风的被全机房吊着打的萌新，她的代码糟糕透了，特别是充实感紧凑美给人带来的视觉震撼程度都比 CK6100LGEV2 不知道差到哪里去了，她用了整整 100 行，而 CK6100LGEV2 只用了 60 行（逃）。

#include <cstdio>
const int maxn = 100005;
int n, m, fa[maxn], son[maxn];
double up[maxn], down[maxn], ans;
struct Edge {
	int to, next, w;
	Edge() {}
	Edge(int to, int next, int w): to(to), next(next), w(w) {}
} e[maxn<<1];
int head[maxn], cnt;
void add(int u, int v, int w) {
	e[++cnt] = Edge(v, head[u], w);
	head[u] = cnt;
}
#define v e[i].to
int pos;
bool vis[maxn], flag;//是否在环上
void dfs1(int u, int k) {
	vis[u] = true;
	for(int i = head[u]; i; i = e[i].next)
		if(v != k) {
			if(vis[v]) { pos = v; return; }
			dfs1(v, u);
			if(!flag and pos) { if(pos == u) flag = true; return; }
			if(flag) break;
		}
	vis[u] = false;
}//将所有环上结点的 vis 标记为 true
int t, disl[22], disr[22], dfn[maxn], path[22];
void dfs2(int u, int k) {
	dfn[u] = ++t, path[t] = u;
	fa[u] = 2;
	for(int i = head[u]; i; i = e[i].next)
		if(v != k and vis[v]) {
			if(!dfn[v]) dfs2(v, u);
			disr[dfn[u]] = disl[dfn[v]] = e[i].w;
			break;
		}
}//处理环上信息
void dp_down(int u, int k) {
	for(int i = head[u]; i; i = e[i].next)
		if(v != k and !vis[v]) {
			fa[v] = 1;
			dp_down(v, u);
			son[u]++;
			down[u] += down[v] + e[i].w;
		}
	if(son[u]) down[u] /= son[u];
}
void dp_up(int u, int k, int w) {
	up[u] = w;
	if(fa[k] + son[k] - 1)
		up[u] += (up[k]*fa[k]+down[k]*son[k]-down[u]-w) / (fa[k]+son[k]-1);
	for(int i = head[u]; i; i = e[i].next)
		if(v != k) dp_up(v, u, e[i].w);
}
void work1() {
	dp_down(1, 0);
	for(int i = head[1]; i; i = e[i].next)
		dp_up(v, 1, e[i].w);
}
double P;
#define nxt(x) (x==t?1:x+1)
#define pre(x) (x==1?t:x-1)
void work2() {
	dfs1(1, 0);
	dfs2(pos, 0);
	for(int i = 1; i <= t; ++i)
		dp_down(path[i], 0);
	for(int i = 1, x; i <= t; ++i) {
		x = path[i];
		P = 0.5;
		for(int j = nxt(i), y; j != i; j = nxt(j)) {
			y = path[j];
			if(nxt(j) == i) up[x] += P * (disl[j]+down[y]);
			else up[x] += P * (down[y]*son[y]/(son[y]+1)+disl[j]);
			P /= (son[y]+1);
		}
		P = 0.5;
		for(int j = pre(i), y; j != i; j = pre(j)) {
			y = path[j];
			if(pre(j) == i) up[x] += P * (disr[j]+down[y]);
			else up[x] += P * (down[y]*son[y]/(son[y]+1)+disr[j]);
			P /= (son[y]+1);
		}
		for(int j = head[x]; j; j = e[j].next)
			if(!vis[e[j].to]) dp_up(e[j].to, x, e[j].w);
	}
}
#undef v
int main() {
	scanf("%d %d", &n, &m);
	for(int i = 1, u, v, w; i <= m; ++i)
		scanf("%d %d %d", &u, &v, &w), add(u, v, w), add(v, u, w);
	if(n != m) work1();//普通树
	else work2();//基环树
	for(int i = 1; i <= n; ++i)
		ans += (down[i]*son[i]+up[i]*fa[i]) / (son[i]+fa[i]);
	printf("%.5lf\n", ans / n);
}