自动搬运

查看原文

来自洛谷，原作者为

	Ice_Kissღ 我已经无路可退

搬运于2025-08-24 21:33:32，当前版本为作者最后更新于2020-08-13 00:22:50，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

简单数学递推，来康康呀

（ 不小心把图片弄挂了，才发现，又补了上来 $QWQ$ 。）

#include<bits/stdc++.h>
using namespace std;
int go(int x,int y)
{
    if (x == 1 && y == 0) { return 3; }
    if (x == 2 && y == 2) { return 4; }
    if(y<=x-y)
    {
    	if(x%2==0) { return x/2+(x/2-y)%2; }
        if(x%2==1) { return (x+1)/2+((x+1)/2-y+1)%2; }
    }
    if(y>x-y) { return go(x+1,y-1); }
}
int main()
{
    int x1,x2,y1,y2;
    cin>>x1>>y1>>x2>>y2;
    int a,b;
    a=max(abs(x1-x2),abs(y1-y2));
    b=min(abs(x1-x2),abs(y1-y2));
    cout<<go(a,b);
    return 0;
}

那话不多说，我们开始吧 $QWQ$ !

题目传送门

1.输入处理

• 首先，题目可以理解为平面直角坐标系上任意一点到另一点走日字

最少需要的次数。哎呀，好像有点麻烦，怎么办呢？

• 其实可以这样，我们取两点横纵坐标之差的绝对值

则直接将原题转化为：

平面直角坐标系中$(0,0)$到第一象限上任意一点走日字最少需要的次数。

不过在这里，我特别让那个任意点的横坐标大于纵坐标。

至于为什么要这样做，之后会讲到。

详细代码：

    int x1,x2,y1,y2;
    cin>>x1>>y1>>x2>>y2;
    int a,b;
    a=max(abs(x1-x2),abs(y1-y2));//a为任意点的横坐标
    b=min(abs(x1-x2),abs(y1-y2));//b为任意点的纵坐标

2.核心递推

• 首先，为了方便大家理解，我将一部分的图画下：

（注：$s3$ 与 $s4$ 共同包含直线 $x=y$,也就是图中白线)

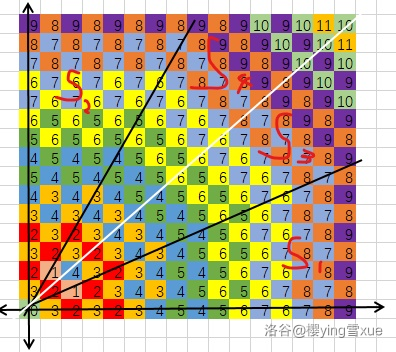
看仔细了，你是否发现了什么！

是不是发现：马从 $(0,0)$ 出发，走 $i$ 步能到达的点恰好可被分为三个区域！

一部分与坐标轴平行（两个区域，每个区域 $4$ 层）；

一部分不与坐标轴平行（为 $3$ 层）不过有特殊点要额外判断。

帮助理解(以 $6$ 为例）：

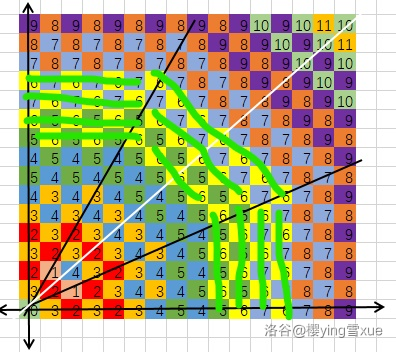
不错不错，可是有三部分窝还是觉得多了，再少点吧 $QAQ$。

所以我特意令 $a$(横坐标) $>$ $b$(横坐标)（易知交换 $ab$ 不改变次数大小)。

则此时我们要讨论的只有两个区间了，也就是 $s1$ 和 $s3$ (见图 $1$ )。

范围缩小了，我们再继续看，会发现一个有趣的事情：

• $s1$ 与 $s3$ 被一条一次函数分开，这个一次函数的表达式为 $y= \dfrac{x}{2}$ 线上的整点恰为次数的递增！！！

例：（ $2$ , $1$ ) — $1$, ( $4$ , $2$ ) — $2$, ( $6$ , $3$ ) — 3, ( $x$ , $\dfrac{x}{2}$ ) — $\dfrac{x}{2}$。

那突破点也找到了，再分类讨论即可：

    if (x == 1 && y == 0) { return 3; }
    if (x == 2 && y == 2) { return 4; }//之前说的特殊情况 。
    if(y<=x-y)//也就是在s1内，通过y<=x/2变换得； 
    {//容易自推出以下两情况 。
    	if(x%2==0) { return x/2+(x/2-y)%2; } 
        if(x%2==1) { return (x+1)/2+((x+1)/2-y+1)%2; }
    }
    if(y>x-y) { return go(x+1,y-1); }
    //也就是在s3内，通过y>x/2变换得。
    //此时我们会发现一个有趣的事情：这个区间内任意一点的值都与它右下角的点相等（见图）；
    //那我们只要不断递推，等到此点落于s1中即可 。
    

最后，完结撒花 $QWQ$ 。

悄悄话：喜欢的话记得点个赞哟 ღღღ 。