自动搬运

查看原文

来自洛谷，原作者为

	墨尔 **

搬运于2025-08-24 21:33:28，当前版本为作者最后更新于2018-06-01 19:33:37，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

写个括号序列的做法。

首先dfs整棵树一遍，进入一个节点的时候加上一个左括号，然后是节点编号，当这个节点的所有子树遍历完后再添上一个右括号，这就是括号序列。（其实就是dfs序加上了括号而已）

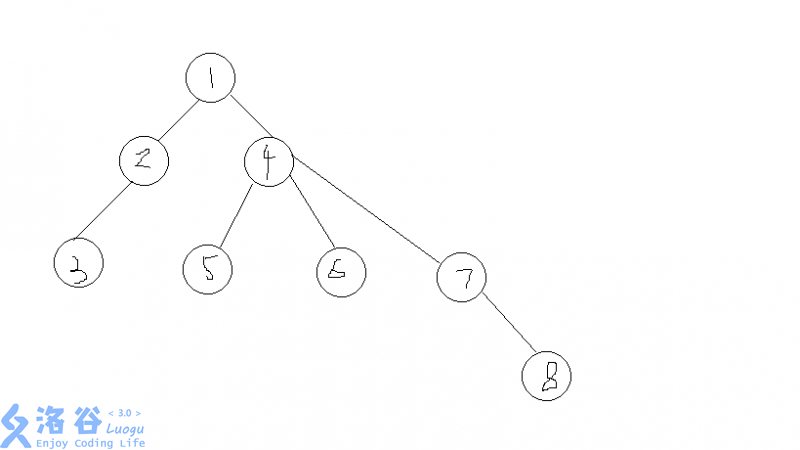
举个栗子，这棵树的括号序列是(1(2(3))(4(5)(6)(7(8))))

我们要求3到8的距离，截取两点间的括号序列为

3))(4(5)(6)(7(8

把编号和匹配的括号删掉

))(((

剩下了5个左右括号，而这就是3到8的距离。

这就是括号序列的性质。

怎么证明？脑补一下，到达i点时

1)添完了左右括号

那个点是i的祖先们的孩子。（不在i到根的路径上）

2）添了左括号没填右括号

那个点是i的祖先。（在i到根的路径上）

3）没添左括号

那个点是i的祖先们的孩子或者i的孩子（不在i到根的路径上）

因此，从s到t，删去的匹配括号们对于s来说是情况3，对于t来说是情况1，很显然这个点不在s到t的路径上。剩下的右括号，对于s来说是情况2，对于t来说是情况1，因此表示从s到达【t到根的这条链】经过的节点数。剩下的左括号，对于s来说是情况3，对于t来说是情况2，因此表示从t到达【s和t的lca（不包括lca）】的经过点数。

综上我们证明了删掉两点间所有匹配括号剩下的左右括号数为距离。

现在我们已经把整棵树压成了一个括号序列了，而我们要求的是两个黑点间的最大距离，我们考虑用线段树求解。

毫无疑问要记录每段区间删掉匹配括号后剩下的左右括号数，我们记右括号数为a，左括号数为b。

【注意我接下来说的所有左右区间都不限于线段树中的左右区间，任意连续的左右区间均可】

左右区间的a、b的合并：

显然左区间的左括号和右区间的右括号合并消去，谁多剩谁

//lc左区间，rc右区间
	if(tr[lc].b>tr[rc].a)
	 tr[id].a=tr[lc].a,tr[id].b=tr[lc].b-tr[rc].a+tr[rc].b;else
	 tr[id].a=tr[lc].a+tr[rc].a-tr[lc].b,tr[id].b=tr[rc].b;

跨区间距离计算：

左区间右左括号数记为a1,b1，右区间a2,b2

dis=a1+abs(b1-a2)+b2=max((a1+b1)+(b2-a2),(a1-b1)+(a2+b2))

显然max(a1+b1),max(b2-a2)这种是可以单独维护的。

因此记录区间前缀的max(a+b),max(b-a)（l1,l2）,后缀的max(a+b),max(a-b)(r1,r2)即可维护dis值

	tr[id].dis=max(max(tr[lc].r1+tr[rc].l2,tr[lc].r2+tr[rc].l1),max(tr[lc].dis,tr[rc].dis));

l1,r1,l2,r2的维护参考合并操作，不解释了自己体会

	tr[id].l1=max(tr[lc].l1,max(tr[rc].l1+tr[lc].a-tr[lc].b,tr[rc].l2+tr[lc].a+tr[lc].b));
	tr[id].l2=max(tr[lc].l2,tr[rc].l2-tr[lc].a+tr[lc].b);
	tr[id].r1=max(tr[rc].r1,max(tr[lc].r1-tr[rc].a+tr[rc].b,tr[lc].r2+tr[rc].a+tr[rc].b));
	tr[id].r2=max(tr[rc].r2,tr[lc].r2+tr[rc].a-tr[rc].b);

因为是要求黑点间的最大距离，显然初始化时白点的l1,r1,l2,r2是没有意义的，置为-inf

至此本题解决。

//括号序列
#include<cstdio>
//(a1 b1)(a2 b2)->(a,b)
//a+b=a1+abs(b1-a2)+b2=max((a1-b1)+(a2+b2),(a1+b1)+(b2-a2))
//需要左区间后缀的max(a-b),max(a+b)，右区间前缀的max(a+b),max(b-a) 
int num,s[300005],pos[1000005],head[100005],n,m,cnt,tot;
bool c[100005];
struct edge{int to,next;}e[200005];
void add(int u,int v){e[++num]=(edge){v,head[u]},head[u]=num;}
struct node
{
	int a,b,l1,l2,r1,r2,dis;
	//a,b右左括号数,l1,l2前缀的max(a+b),max(b-a),r1,r2后缀的max(a+b),max(a-b)  
}tr[1200005];
void dfs(int u,int fa)
{
	s[++tot]=-1;//左括号
	s[++tot]=u;pos[u]=tot;
	for(int i=head[u];i;i=e[i].next)
	{
		int v=e[i].to;if(v==fa)continue;
		dfs(v,u);
	}
	s[++tot]=-2;//右括号 
}
void push(int id,int x)
{
	tr[id].a=tr[id].b=0;tr[id].l1=tr[id].l2=tr[id].r1=tr[id].r2=tr[id].dis=-1e9;
	if(s[x]==-1)tr[id].b=1;else
	if(s[x]==-2)tr[id].a=1;else
	if(!c[s[x]])tr[id].l1=tr[id].r1=tr[id].r2=tr[id].l2=0;//黑点 
}
int max(int a,int b){return a>b?a:b;}
void merge(int id)
{
	int lc=id<<1,rc=id<<1|1;
	if(tr[lc].b>tr[rc].a)
	 tr[id].a=tr[lc].a,tr[id].b=tr[lc].b-tr[rc].a+tr[rc].b;else
	 tr[id].a=tr[lc].a+tr[rc].a-tr[lc].b,tr[id].b=tr[rc].b;
	tr[id].l1=max(tr[lc].l1,max(tr[rc].l1+tr[lc].a-tr[lc].b,tr[rc].l2+tr[lc].a+tr[lc].b));
	tr[id].l2=max(tr[lc].l2,tr[rc].l2-tr[lc].a+tr[lc].b);
	tr[id].r1=max(tr[rc].r1,max(tr[lc].r1-tr[rc].a+tr[rc].b,tr[lc].r2+tr[rc].a+tr[rc].b));
	tr[id].r2=max(tr[rc].r2,tr[lc].r2+tr[rc].a-tr[rc].b);
	tr[id].dis=max(max(tr[lc].r1+tr[rc].l2,tr[lc].r2+tr[rc].l1),max(tr[lc].dis,tr[rc].dis));
}
void build(int id,int l,int r)
{
	if(l==r){push(id,l);return;}
	int mid=l+r>>1;
	build(id<<1,l,mid);build(id<<1|1,mid+1,r);
	merge(id);
}
void modify(int id,int l,int r,int x)
{
	if(l==r){push(id,l);return;}
	int mid=l+r>>1;
	if(x<=mid)modify(id<<1,l,mid,x);else modify(id<<1|1,mid+1,r,x);
	merge(id);
}
int main()
{
	scanf("%d",&n);
	for(int i=1,u,v;i<n;i++)
	{
		scanf("%d%d",&u,&v);
		add(u,v),add(v,u);
	}
	dfs(1,0);cnt=n;
	build(1,1,tot); 
	scanf("%d",&m);
	for(int i=1,x;i<=m;i++)
	{
		char s[2];
		scanf("%s",s);
		if(s[0]=='C')scanf("%d",&x),cnt+=c[x]?1:-1,c[x]^=1,modify(1,1,tot,pos[x]);
		else if(cnt==0)printf("-1\n");else if(cnt==1)printf("0\n");else
		printf("%d\n",tr[1].dis);
	}
}