自动搬运

查看原文

来自洛谷，原作者为

	顾z 得之我幸，失之我命

搬运于2025-08-24 21:33:25，当前版本为作者最后更新于2018-10-04 06:20:00，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题目描述

这次小可可想解决的难题和中国象棋有关，在一个N行M列的棋盘上，让你放若干个炮（可以是0个），使得没有一个炮可以攻击到另一个炮，请问有多少种放置方法。大家肯定很清楚，在中国象棋中炮的行走方式是：一个炮攻击到另一个炮，当且仅当它们在同一行或同一列中，且它们之间恰好 有一个棋子。你也来和小可可一起锻炼一下思维吧！

40pts

考试遇到了这个题,玄学打表得了$40pts$

玄学打表吼啊

xjb分析

正解竟然是个$DP$? 还有人说是状压$DP$?哪里来的状压啊!

前置知识

考虑到我们的合法状态的话,每一行每一列的炮的数量$\le 2$

(炮打隔重山?) 显然 如果一行或者一列有三个炮的话将会不合法.(两个炮可以互相打啊 qwq)

如何设状态?

因为每一行每一列的炮的数量$\leq 2$

所以我们考虑记数组去存储有几列放了一个炮,有几列放了两个炮.

我们又需要考虑转移?

因此设出状态

$f[i][j][k]$代表放了前$i$行,有$j$列是有一个棋子,有$k$列是有2个棋子的合法方案数.

这个时候我们知道全部的列数,又知道一些情况的列数.

所以我们可以求出不放棋子的列数

单步容斥：空的=全部的$-$合法的

即空的序列$=m-j-k$

确定情况

1. 我们可以在当前第$i$行不放棋子.
2. 我们可以在当前第$i$行放一个棋子
3. 我们可以在当前第$i$行放两个棋子.

接下来就需要分类讨论这些情况.

分类讨论

一.不放棋子

我们可以直接继承上面的状态.即

$$f[i][j][k]=f[i-1][j][k]$$

二.放一个棋子

显然我们不会选择放在有两个棋子的列.

因此存在情况如下

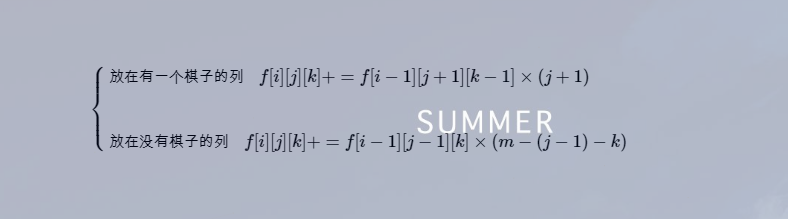
解释：

放在一个棋子的列

我们在某一个有一个棋子列放置棋子,会使这一列变为有两个棋子.

即我们要得到$f[i][j][k]$需要在$j+1$个有一个棋子的列放置棋子,变为$j$个有一个棋子的列

而我们又会得到一个新的有两个棋子的列.因此我们之前必须有$k-1$个有两个棋子的列.

即$f[i-1][j+1][k-1]$的状态可以传递给$f[i][j][k]$

而我们又可以在$(j+1)$中的任何一列放置这一个棋子.

因此我们要$\times (j+1)$

放在没有棋子的列

在一个没有棋子的列放置棋子,我们会得到一个新的有一个棋子的列.

即我们要从$j-1$得到$j$.

而这个时候,我们有两个棋子的列的数量不会变,所以从$k$传递即可.

即$f[i-1][j-1][k]$的状态可以传递给$f[i][j][k]$

又因为我在空列中的任何一列放置这个棋子.

所以要$\times$ $(m-(j-1)-k)$

三.放两个棋子

这个时候情况会多一个.先请大家自己考虑一下.

这个时候存在情况如下

解释

一个放在有一个棋子的列,一个放在没有棋子的列

这个时候,我们放置之后 :

一个没有棋子的列会变成一个有一个棋子的列,而一个有一个棋子的列会变成一个有两个棋子的列。

此时我们发现,

​ 有一个棋子的列的数量不会变,因此第二维依旧为$j$，

​ 又因为我们会新增一个有两个棋子的列,所以我们需要从$k-1$转移过来.

又因为我们可以在有一个棋子的列随便放,空列随便放.

根据乘法原理,需要$\times j \times (m-j-(k-1))$

都放在没有棋子的列

此时我们放置之后

​ 会增加两个新的有一个棋子的列.

因此我们需要从$j-2$转移过来.

而两个棋子的列的数量并不会改变,所以依旧为$k$

又因为在空列中我们随便放.

根据组合数学,需要$\times C_{m-(j-2)-k}^{2}$

都放在有一个棋子的列

我们放置在有一个棋子的列之后：

​ 这两个有一个棋子的列都会变成有两个子的列.

​ 即$j+2$变成$j$，从$k-2$变成$k$

又因为这些有一个棋子的列我们随便选择.

根据组合数学,需要$\times C_{j+2}^{2}$

分析完毕

我们需要接下来做的就是判断边界,一定要判断!!(血的教训!

代码

#include<cstdio>
#include<cstring>
#include<cmath>
#include<cctype>
#include<cstring>
#define mod 9999973
#define int long long
#define R register
using namespace std;
inline  void in(int &x)
{
	int f=1;x=0;char s=getchar();
	while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
	while(isdigit(s)){x=x*10+s-'0';s=getchar();}
	x*=f;
}
int n,m,ans;
int f[108][108][108];
inline int C(int x)
{
	return ((x*(x-1))/2)%mod;
}
signed main()
{
	in(n),in(m);
	f[0][0][0]=1;
	for(R int i=1;i<=n;i++)
	{
		for(R int j=0;j<=m;j++)
		{
			for(R int k=0;k<=m-j;k++)
			{
				f[i][j][k]=f[i-1][j][k];
				if(k>=1)(f[i][j][k]+=f[i-1][j+1][k-1]*(j+1));
				if(j>=1)(f[i][j][k]+=f[i-1][j-1][k]*(m-j-k+1));
				if(k>=2)(f[i][j][k]+=f[i-1][j+2][k-2]*(((j+2)*(j+1))/2));
				if(k>=1)(f[i][j][k]+=f[i-1][j][k-1]*j*(m-j-k+1));
				if(j>=2)(f[i][j][k]+=f[i-1][j-2][k]*C(m-j-k+2));
				f[i][j][k]%=mod;
			}
		}
	}
	for(R int i=0;i<=m;i++)
		for(R int j=0;j<=m;j++)
			(ans+=f[n][i][j])%=mod;
	printf("%lld",(ans+mod)%mod);
}