自动搬运

查看原文

来自洛谷，原作者为

	MRCMRC 缘起缘灭，相识梦一场。行走天涯路不同，自当离别时

搬运于2025-08-24 21:32:56，当前版本为作者最后更新于2019-04-14 17:49:59，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

计算几何水好题

读明题意后，我们可以画出以下这张图(借用样例说明)：

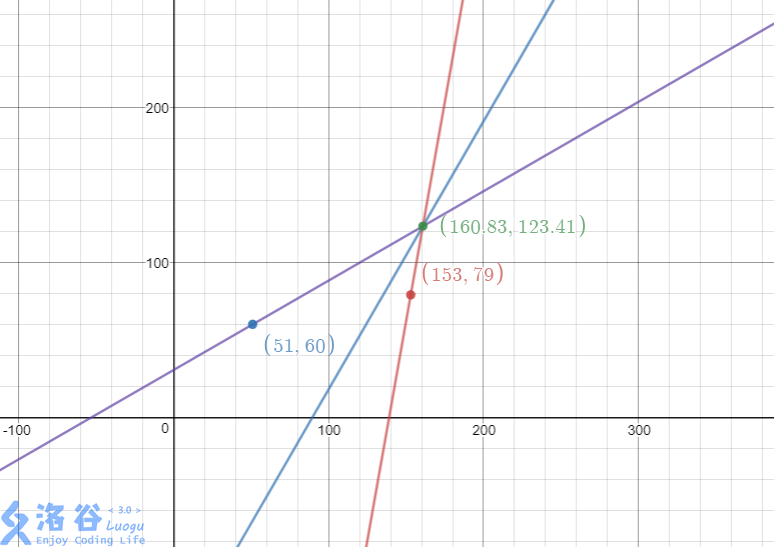
(其中，蓝色的直线为船的航线所在的直线

紫色与红色为灯塔相对于船的方位)

不难看出，其实就是已知两条直线，求出直线的交点，即为船当前的位置！！

由平面几何中直线的定义，我们知道，对于函数$f(x)$，它有一种形式叫做点斜式；

然后根据斜率的定义，我们可以求得一条直线的斜率可以以两个直线上的点的坐标决定：

那么则有：

$$tanα=\frac{y_1-y}{x_1-x}$$ $$(x_1-x)\cdot tanα=y_1-y$$ $$y=y_1-(x_1-x)\cdot tanα$$

将$y$分别由$x_1$，$y_1$，$x_2$，$y_2$表示得：

$$\left\{\begin{matrix}y=y_1-(x_1-x)\cdot tan\alpha &\\y=y_2-(x_2-x)\cdot tan\beta &\end{matrix}\right. $$

联立，得：

$$y_1-(x_1-x)=y_2-(x_2-x)$$

移项，得：

$$y_1-x_1tan\alpha+xtan\alpha=y_2-x_2tan\beta+xtan\beta $$$$x(tan\alpha-tan\beta)=y_2-y_1+x_1tan\alpha-x_2tan\beta $$$$x=\frac{y_2-y_1+x_1tan\alpha-x_2tan\beta}{tan\alpha-tan\beta} $$

所以，我们只需要对于每条直线，处理出它们的斜率(即$tan\alpha$，$\alpha$为直线与$x$轴倾斜角)

我们知道，题目给出的是航线与直线的夹角，而航线的方位是相对于$y$轴的夹角：

我们只需要求得该夹角的余角，即$90^{\circ}-\theta$($\theta$为给出的夹角)。

同时，对于直线的倾斜角，我们处理它对于$x$轴的夹角时，是允许存在第四象限角的，即斜率为负。

所以我们这样处理：

double beta=180-an-an2;

其中$an$为航线的倾斜角，$an1$，$an2$分别表示两条位置所在的直线的夹角；

另外，当两直线斜率相同，则无解。

完整代码：

#include<bits/stdc++.h>
#define in inline
#define reg register
#define int long long
#define MAX 20030813
#define pi acos(-1)
using namespace std;
namespace qwq{
	in int read(int &o)
	{
		o=0;
		int w=1;
		char c=getchar();
		while(c<'0'||c>'9')
		{
			if(c=='-')w=-1;
			c=getchar();
		}
		while(c>='0'&&c<='9')
		{
			o=(o<<3)+(o<<1)+(c^48);
			c=getchar();
		}
		return o*w;
	}
	in void write(int x)
	{
    	if(x>9)write(x/10);
    	putchar(x%10+48);
	}
	in int max(int x,int y)
	{
		return x>y?x:y;
	}
	in int min(int x,int y)
	{
		return x<y?x:y;
	}
}
using namespace qwq;
int n;
class Tower
{
public:
	int x,y;
	char cnt;
}tow[MAX];
char c1,c2;
double _x1_,_x2_,_y1_,_y2_,x,y;
int alpha,beta,an,an1,an2;
signed main()
{
	read(n);
	for(reg int i=1;i<=n;++i)
	{
		cin>>tow[i].cnt;
		read(tow[i].x),read(tow[i].y);
	}
	read(an);
	an-=90;
	cin>>c1,read(an1);
	alpha=180-an-an1;
	cin>>c2,read(an2);
	beta=180-an-an2;  
        if(tan(pi/180*alpha)==tan(pi/180*beta))
        {
        	puts("NO ANSWER");return 0;
        }
	for(reg int i=1;i<=n;++i)
	{
		if(c1==tow[i].cnt)_x1_=tow[i].x,_y1_=tow[i].y;
		if(c2==tow[i].cnt)_x2_=tow[i].x,_y2_=tow[i].y;
	}
	x=((_y2_-_y1_)+_x1_*tan(pi/180*alpha)-_x2_*tan(pi/180*beta))/(tan(pi/180*alpha)-tan(pi/180*beta));
	y=_y1_+(x-_x1_)*tan(pi/180*alpha);
	printf("%.2lf %.2lf\n",x,y);
	return 0;
}

在楼上两篇大佬的题解里，对于灯塔位置的映射是用$map$实现的，然而此题灯塔数量$n\leq30$，在下认为是不需要$map$的，直接 $\Theta (n)$扫描不就好啦？

若路过大佬在此停留，指点一二，蒟蒻不胜感激

Update in 19.8.15：感谢@RsXxy对于本文错误的指正。