1 条题解
-
0
自动搬运
来自洛谷,原作者为

P_E_K_K_A
山不厌高,海不厌深,周公吐哺,天下归心搬运于
2025-08-24 21:32:55,当前版本为作者最后更新于2021-12-01 13:51:22,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
(Update:修改了乘号)
1道电学好题前置知识:高斯消元
分析
观察样例:
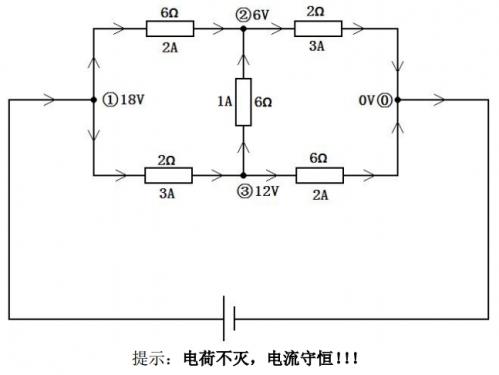
对于一个 (比如图中的②):令电流流入 的节点记为 ; 电流流出 的节点为 。容易知道:
(流入的电流之和等于流出的电流之和)
因为:
(但愿你学过初中电学)
所以:
(这里的 和 指的是 或 到 这段导体的电压和电阻,因为我们习惯于考虑一段电阻而不是两个点的电势差)
我们知道,但是 怎么知道呢?
如果你学习过一定高中物理,你会知道电压其实就是两个位置之间电势的差值,所以设节点 的电势为 则
式子变成:
$\sum_{A_i}\frac{curU_A-curU_Q}{R_A}=\sum_{Bi}\frac{curU_Q-curU_B}{R_B}$
移项:
$\sum_{A_i}\frac{curU_A-curU_Q}{R_A}+\sum_{Bi}\frac{curU_B-curU_Q}{R_B}=0$
令即:
于是你惊喜地发现:不需要判断电流方向了!
但知道这个式子有什么用呢?
解决(代码)
由式子想到列方程(高斯消元),设每个点的电势为未知量,讯问时直接作差即可
变形:
$\sum_{S_i}curU_S \times \frac{1}{R_S} - curU_Q \times \sum_{S_i}\frac{1}{R_S}=0$
所以如果节点 与 直接相连,那么在以 主元的方程中 的系数为
而对于以 主元的方程,的系数为
核心代码(带注释):
for(register int i=1;i<=m;i++) { int u,v;db w; u=read(),v=read(),w=read(); add(u,v,w),add(v,u,w);//建立电路图 } //列方程(核心) for(register int i=1;i<=n;i++) { if(st[i]) k[i][i]=1,k[i][n+1]=st[i]; //st[i]是正电极电势 //如果是正电极那么方程直接为 1*U[i]=st[i] else { db sum=0; for(int j=head[i];j;j=Edge[j].nxt) { int v=Edge[j].v;db w=Edge[j].w; k[i][v]+=1.0/w;//注意可能两点间有多个电阻 sum+=1.0/w; } k[i][i]=-sum;//主元的系数 } } gouse();//自行添加正确性:每个未知量都有主元的方程(即一共 个),肯定能解出来
时间复杂度:
O(能过)列方程 O() 高斯消元O( )总:O()
制作不易,望管理员大大通过(这道题还没有较为详细的题解)
QwQ 完结撒花~~~
- 1
信息
- ID
- 976
- 时间
- 1000ms
- 内存
- 125MiB
- 难度
- 6
- 标签
- 递交数
- 2
- 已通过
- 0
- 上传者
