自动搬运

查看原文

来自洛谷，原作者为

	Infinite_Eternity 『放肆梦一场，谁说永夜中照不进天光，当乌云散去，自有漫天繁星』

搬运于2025-08-24 21:32:45，当前版本为作者最后更新于2022-12-15 15:59:10，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

Description

P1995 [NOI2011] 智能车比赛

给定 $n$ 个矩形区域，每个矩形的边都平行于坐标轴，第 $i$ 个矩形区域的左下角和右上角坐标分别为 $(x_{i,1},y_{i,1})$ 和 $(x_{i,2},y_{i,2})$。给定起点 $S$，终点 $T$，速度 $v$，求：从起点 $S$ 到终点 $T$ 的最短时间为多少。

数据范围：$n \leq 2 \times 10^3$，$|x_{i,1}|,| y_{i,1}|, |x_{i,2}|,|y_{i,2}| \leq 4 \times 10^4$

Analysis

看很多大佬的解法都是 dp，但好像都被 Hack 了（？

• Hack 第一篇题解
• Hack 第二篇题解
• Hack 第三篇题解
• Hack 第四篇题解
• Hack 第五篇题解

我的做法是：构图 $+$ SPFA。

首先，我们要找到关键点。关键点包括起点，终点，和相邻矩形接触线段的上端点和下端点（如下图，有红色圈住的点即为关键点）。

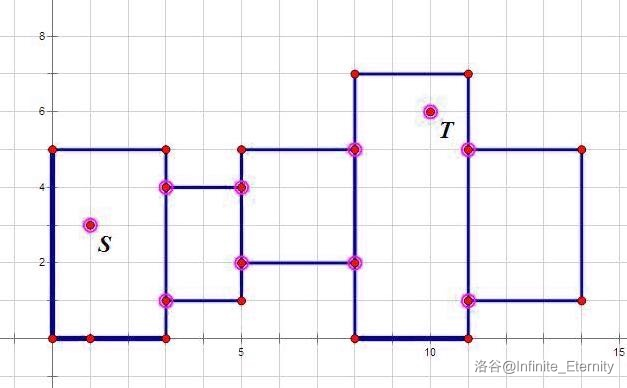
接下来，我们要做的就是在这些关键点之间连边。

我们把这些关键的点拿出来：

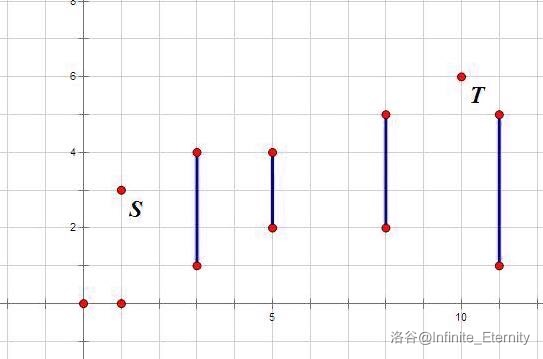
不难发现，其实就是一些竖直的线段。

除了起点 $S$ 和终点 $T$ 外，从左到右或者从右到左穿过线段所在的直线，必须在线段中穿过去，也就是说有个上边界和下边界。

下图是起点 $S$ 到第 $4$ 条竖直的线段的上边界 $l_1$ 和下边界 $l_2$。

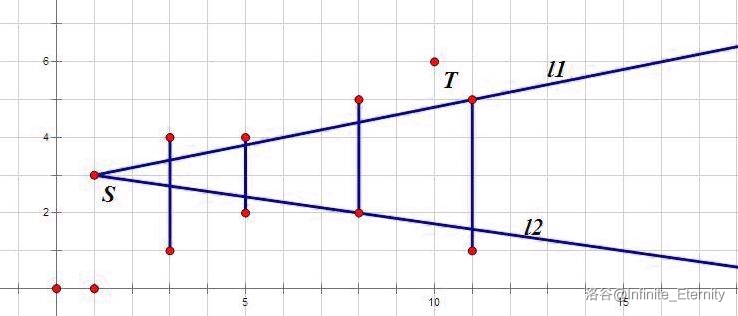
然后，我们先按 $x$ 坐标从小到大排序，枚举边的起点，向左或者向右连边，如果遇到竖直的线段，用叉积更改上下边界即可。

最后，构好图就直接 SPFA 即可。

Code

码风不怎么好看，不喜勿喷。

#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>

using namespace std;

const int maxN=2000;
const double INF=1e15;
const double EPS=1e-9;

inline int dblcmp(double x)
{
    if (abs(x)<EPS)return 0;
    return x>0?1:-1;
}
inline double sqr(double x)
{
    return x*x;
}

struct Tpoint
{
    double x,y;
    inline Tpoint() {}
    inline Tpoint(double _x,double _y)
    {
        x=_x;
        y=_y;
    }
};

inline double dis(Tpoint a,Tpoint b)
{
    return sqrt(sqr(a.x-b.x)+sqr(a.y-b.y));
}
inline double det(Tpoint p0,Tpoint p1,Tpoint p2)
{
    return (p1.x-p0.x)*(p2.y-p0.y)-(p1.y-p0.y)*(p2.x-p0.x);
}

int N;
Tpoint square[maxN+100][2];
Tpoint a[maxN+100][2];
int id[maxN+100][2],cnt;
int now,info[2*maxN+100];
struct Tedge
{
    int v,next;
    double dis;
} edge[2*maxN*2*maxN+1000];
double ans,v;
Tpoint S,T;
int eS,eT,idS,idT;

inline void addedge(int u,int v,double dis)
{
    now++;
    edge[now].v=v;
    edge[now].dis=abs(dis);
    edge[now].next=info[u];
    info[u]=now;
}

inline void solve(Tpoint s,int num,int l)
{
    if (num!=idS && num!=idT && num%2==0)
    {
        addedge(num,num+1,dis(a[l][0],a[l][1]));
        addedge(num+1,num,dis(a[l][0],a[l][1]));
    }
    Tpoint low,high,t1,t2;
    bool flag=0;
    for(int i=l-1; i>=1; --i)
    {
        if (!flag && (id[i][0]==idS || id[i][0]==idT))
        {
            addedge(num,id[i][0],dis(s,a[i][0]));
            addedge(id[i][0],num,dis(s,a[i][0]));
            continue;
        }
        if (!flag)
        {
            addedge(num,id[i][0],dis(s,a[i][0]));
            addedge(id[i][0],num,dis(s,a[i][0]));
            addedge(num,id[i][1],dis(s,a[i][1]));
            addedge(id[i][1],num,dis(s,a[i][1]));
            low=a[i][0];
            high=a[i][1];
            flag=1;
            continue;
        }
        t1=a[i][0];
        t2=a[i][1];
        if ( dblcmp(det(s,low,t1))<=0 && dblcmp(det(s,high,t1))>=0 )
        {
            addedge(num,id[i][0],dis(s,a[i][0]));
            addedge(id[i][0],num,dis(s,a[i][0]));
        }
        if ( dblcmp(det(s,low,t2))<=0 && dblcmp(det(s,high,t2))>=0 )
        {
            addedge(num,id[i][1],dis(s,a[i][1]));
            addedge(id[i][1],num,dis(s,a[i][1]));
        }
        if (id[i][0]!=idS && id[i][0]!=idT)
        {
            if ( dblcmp( det(s,low,t2) ) == 1 ) break;
            if ( dblcmp( det(s,high,t1)) == -1 ) break;
            if ( dblcmp( det(s,low,t1) ) == -1 ) low=t1;
            if ( dblcmp( det(s,high,t2))== 1 ) high=t2;
        }
    }
}

int head,tail,queue[7*2*maxN+100];
bool vis[2*maxN+100];
double f[2*maxN+100];
inline double SPFA()
{
    int S=idS,T=idT;
    for(int i=1; i<=cnt; ++i) f[i]=INF;
    queue[head=tail=0]=S;
    f[S]=0.0;
    vis[S]=1;
    while(head<=tail)
    {
        int u=queue[(head++)%(7*2*maxN+100)],v,i;
        double dis;
        vis[u]=0;
        for(i=info[u],v=edge[i].v,dis=edge[i].dis; i!=-1; i=edge[i].next,v=edge[i].v,dis=edge[i].dis)
            if ( dblcmp(dis+f[u]-f[v])==-1 )
            {
                f[v]=dis+f[u];
                if (!vis[v])
                {
                    vis[v]=1;
                    queue[(++tail)%(7*2*maxN+100)]=v;
                    if ( dblcmp(f[queue[head%(7*2*maxN+100)]]-f[queue[tail%(7*2*maxN+100)]])==1 ) swap(queue[tail%(7*2*maxN+100)],queue[head%(7*2*maxN+100)]);
                }
            }
    }
    return abs(f[T]);
}

int main()
{
    //freopen("car.in","r",stdin);
    //freopen("car.out","w",stdout);
    scanf("%d\n",&N);
    for(int i=1; i<=N; ++i)scanf("%lf%lf%lf%lf\n",&square[i][0].x,&square[i][0].y,&square[i][1].x,&square[i][1].y);
    scanf("%lf%lf\n",&S.x,&S.y);
    for(int i=1; i<=N; ++i)
        if (dblcmp(square[i][0].x-S.x)<=0 && dblcmp(S.x-square[i][1].x)<=0 && dblcmp(square[i][0].y-S.y)<=0 && dblcmp(S.y-square[i][1].y)<=0)
        {
            eS=i;
            break;
        }
    scanf("%lf%lf\n",&T.x,&T.y);
    for(int i=1; i<=N; ++i)
        if (dblcmp(square[i][0].x-T.x)<=0 && dblcmp(T.x-square[i][1].x)<=0 && dblcmp(square[i][0].y-T.y)<=0 && dblcmp(T.y-square[i][1].y)<=0)
        {
            eT=i;
            break;
        }
    int g=N;
    N=0;
    for(int i=1; i<=g; ++i)
    {
        if (i==eS)
        {
            N++;
            a[N][0].x=S.x;
            a[N][0].y=S.y;
            a[N][1].x=S.x;
            a[N][1].y=S.y;
            idS=id[N][0]=id[N][1]=++cnt;
        }
        if (i==eT)
        {
            N++;
            a[N][0].x=T.x;
            a[N][0].y=T.y;
            a[N][1].x=T.x;
            a[N][1].y=T.y;
            idT=id[N][0]=id[N][1]=++cnt;
        }
        if (i==g) continue;
        N++;
        a[N][0].x=square[i][1].x;
        a[N][0].y=max(square[i][0].y,square[i+1][0].y);
        a[N][1].x=square[i][1].x;
        a[N][1].y=min(square[i][1].y,square[i+1][1].y);
        id[N][0]=++cnt;
        id[N][1]=++cnt;
    }
    memset(info,-1,sizeof(info));
    now=-1;
    for(int i=2; i<=N; ++i)
        for(int j=0; j<2; j++)
            solve(a[i][j],id[i][j],i);
    ans=SPFA();
    scanf("%lf\n",&v);
    ans=ans/v;
    printf("%0.10lf\n",ans);
    return 0;
}