自动搬运

查看原文

来自洛谷，原作者为

	info___tion 統一祖國，振興中華！

搬运于2025-08-24 21:32:42，当前版本为作者最后更新于2018-04-05 00:18:40，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

这道题其实就是一道递推题目，但它的递推公式又很复杂。

不得不说，前面两位DALAO的解法都是对的，但他们没有讲到他们写的状态转移方程是怎么来的，所以这应该会让很多蒟蒻（包括笔者本人）一脸懵逼~~~。所以本人打算详细地讲一讲这一题。

下面开始进入题解：

---

首先，既然是递推，那么分好状态就是一件非常重要的事情。这里本人直接讲状态。

（下文中的F[N]表示铺满前N*2的面积的墙的方案数；“一列”指长为1，宽为2的墙壁）

---

1.当这面墙的最后一列被铺满时（如下图所示）

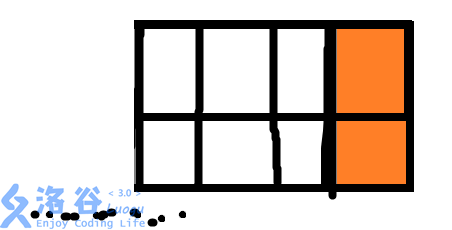
以这种状态结尾的方案数为F[N-1]。

---

2.当这面墙的最后两列被铺满时（如下图所示，注意颜色的区别）

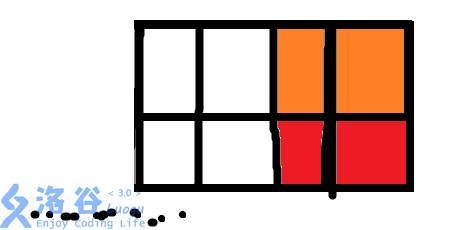
以这种状态结尾的方案数为F[N-2]。

---

大家也看到，前两种状态很容易想到，也很容易描述。

但是，L形的瓷砖又怎么办呢？

（呵呵，刚开始想到这里的时候，我自己都蒙了。）

为了方便大家思考，我们先往简单的方向想。（以下是重点！！！）

---

我们可以用一个数组G[N]来表示**铺满前(N+1)*2的面积的墙，但是第(N+1)列有一个瓷砖已经被铺过（注意，是已经被铺过！）**的方案数。

所以，L形瓷砖的问题就已经被“初步”解决了。

所以，下面这种情况的方案数就是G[N-2]（因为实际上第N列已经铺满了，所以这里要处理的是前N-1列墙，所以多减了1）（如下图所示）:

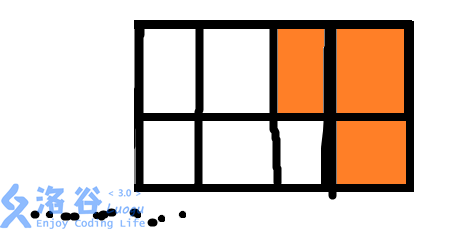
同理，这一种情况的方案数也是G[N-2]：

---

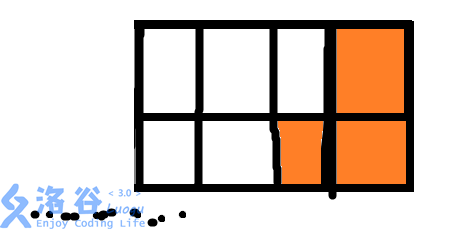
OK,现在问题来了：这个G数组应该怎么维护呢？

不急，我们可以画图。

首先，第一种情况就是直接先让它变成一个长方形：

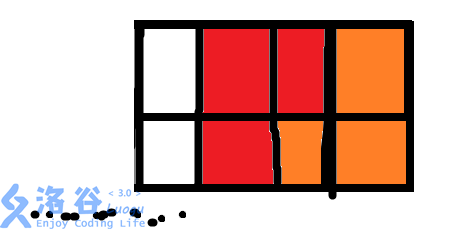
以这种状态结尾的方案数为F[N-3]。

第二种情况是，加上一块砖后，它仍然不是一个长方形：

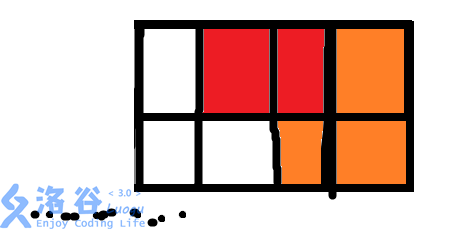
so,这第二种情况的方案数就是G[N-3]（可能需要转一下弯，希望大家能弄懂）。

所以，G[N-2]（注意，不是G[N]）的方案数就等于F[N-3]+G[N-3]。

稍微化简一下，就可以得出：G[N]=F[N-1]+G[N-1]。

---

所以，F[N]的转移方程就是：

F[N]=F[N-1]+F[N-2]+2*G[N-2]（别忘了前面讲过G[N-2]的情况有两种）

而G[N]的转移方程就是：G[N]=F[N-1]+G[N-1]。

初始化：F[0]=1,G[0]=0;F[1]=G[1]=1;

以下献上代码：

#include<iostream>
using namespace std;

const int maxn=1000002;
const int mod=10000;

int f[maxn],g[maxn];

int main()
{
	int n;
	
	cin>>n;
	
	f[0]=1;	//g[0]=0
	
	f[1]=g[1]=1;
	
	for(int i=2;i<=n;i++)
	{
		f[i]=((f[i-1]+f[i-2])%mod+2*g[i-2]%mod)%mod;
		
		g[i]=(g[i-1]+f[i-1])%mod;
	}
	
	cout<<f[n];
	
	return 0;
}

---

总而言之，这道题目所涉及的算法并不复杂，但很考验各位OIer的思维能力（特别是分类讨论和转化思想），这是一道好题！