自动搬运

查看原文

来自洛谷，原作者为

	WHUSHZ **

搬运于2025-08-24 21:32:32，当前版本为作者最后更新于2019-10-15 04:18:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目分析

特例分析

我们先来考虑 $4$ 个点的情形

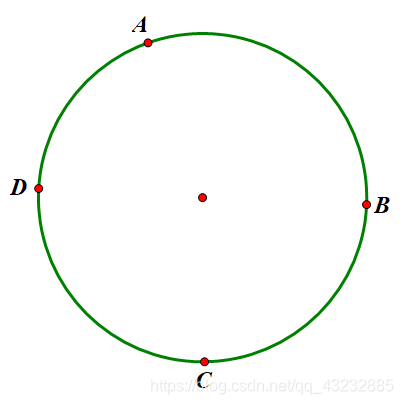
显然有以下 $2$ 种方案：[$AD$，$BC$]，[$AB$，$CD$].

再考虑一下 $6$ 个点的情形

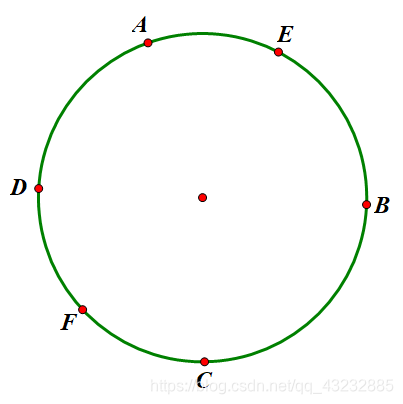
其实由于连线不会相互交叉，每一次连线，相当于在饼上切了一刀，将饼分为两部分，我们可以照着操作一下。

首先假设我们第一刀切 $BE$，那么这块饼分成了两部分，一部分上还有4个点可供切割，另一部分0个点可供切割，而由于 $BE$ 已经被切过，这两个点接下来应该不计入考虑，事实上我们把问题分解成了两部分，即圆上4个点和圆上0个点的情形.

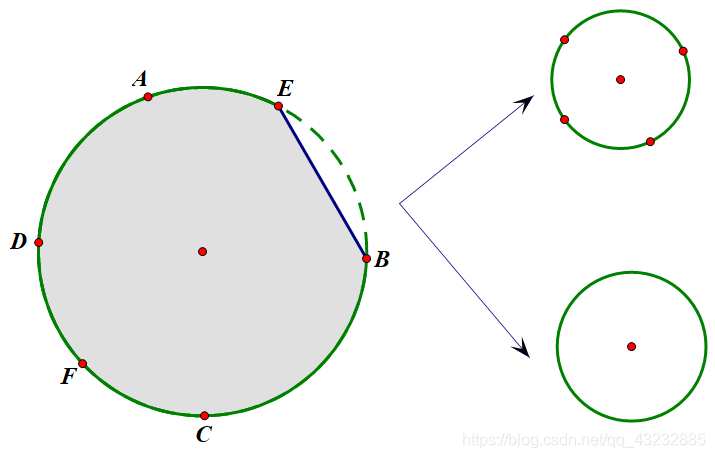
这一种情形下的切法数为 $2\times 1=2$ 种.

如果第一步沿 $EC$ 或者 $ED$ 切，则连不满 $N$ 根线.

如果第一步沿 $EA$ 切，则切法仍为$2\times 1=2$ 种.

如果第一步沿 $EF$ 切，显然只剩下 $1$ 种.

显然我们已经算完了所有不重复的结果，因此 $6$ 个点时有 $5$ 种方法.

一般情况

那么如果有 $2N$ 个点呢？

根据以上我们得出，如果第一刀，使得分成的两半上均只有奇数个点，将连不满 $N$ 根线，换言之，此时满足要求的切法为 $0$.

假设，圆上有 $2k$ 个点时，切法为 $f(k)$，那么根据第一刀分成的左右两边的点的个数，由加法原理以及乘法原理可以得到

这里注意，一旦点的分布确定了，第一刀左侧为$N$，右侧为 $0$和左侧为 $0$，右侧为 $N$ 将指向不同的结果，看我们之前对于 $6$ 个点的情况分析，我们先取定一个点作为初始点，事实上这个点是任意选的，假定点的编号从小到大顺时针排序，连 $A_1A_2$ 即为左 $N$ 右 $0$，连 $A_1A_{N+1}$ 则相反. 可以看出，前者的组合里面，无论哪一种，都不可能含有 $A_1A_{N+1}$，而后者的组合也都不可能含有 $A_1A_2$，因此这两种方案是不同的.

那么既然初始点的选择是任意的，我们是否需要为此乘上 $2N$ 或者 $N$ 之类的系数呢？

我们还是回到 $6$ 个点的分析中去，倘若我们选择 $BC$ 作为第一刀，结果又将如何呢？答案是结果完全一样，无论是数量还是切法，都将保持一致.

我们以集合的角度进行思考，一种切法中的所有弦构成一个集合，所有的切法集合构成全集 $U$，所以其实定弦是一种遍历的方式，首先圆上所有的点都要被连到，那也就意味着所有的切法里面必然含有所有点，那么如果我们选定一个有特征的点 $A$，作为起始点，这个起始点是非特异的，而作为 $A$ 这个点而言，和周围的点也只有 $N$ 种连接方式，我们考虑了这 $N$ 种连接方式的全体，相当于是对这个集合做了一次遍历，既然是遍历，也即意味着选一个点即可计算出全体，而不是一种特例，所以不用乘以任何系数。

所以本道题的答案就是第 $N$ 个卡特兰数. 贴上AC代码吧。

#include<iostream>  
#include<cstring>
using namespace std;  
int main() {  
    unsigned long long ctl[32768], i, j, k, n;  
    memset(ctl, 0, sizeof(ctl));  
    ctl[0] = ctl[1] = 1;ctl[2] = 2;  
    cin >> n;  
    for (i = 3; i <= n; ++i)  
        for (j = 0; j < i; ++j) {  
            ctl[i] += ctl[j] * ctl[i - j - 1];  
            ctl[i] %= 100000007;  
        }  
    cout << ctl[n];  
    return 0;  
}