自动搬运

查看原文

来自洛谷，原作者为

	Strong_Jelly **

搬运于2025-08-24 21:32:20，当前版本为作者最后更新于2019-06-11 10:50:49，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

我们用拓扑排序来做这道题

先讲解一下拓扑排序：

拓扑排序是用来解决AOV网的问题的一个算法

AOV网是一个无环有向图，形象的解释一下：一个农夫有n项农活要干，但农活是有先后顺序的（例如必须先给庄稼施肥，浇水，最后才能采摘，总不能拔苗助长啊）。我们可以用一个图来形象的描绘出来（必须先完成的农活A指向必须完成A这个农活才可以做的农活B，以此构成一个图），这就是AOV网。

给张图形象一下，就不口胡了

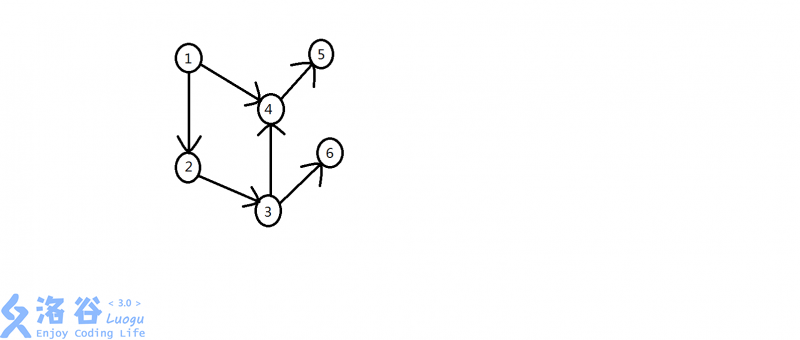
无环是因为有环就会发生冲突，例：

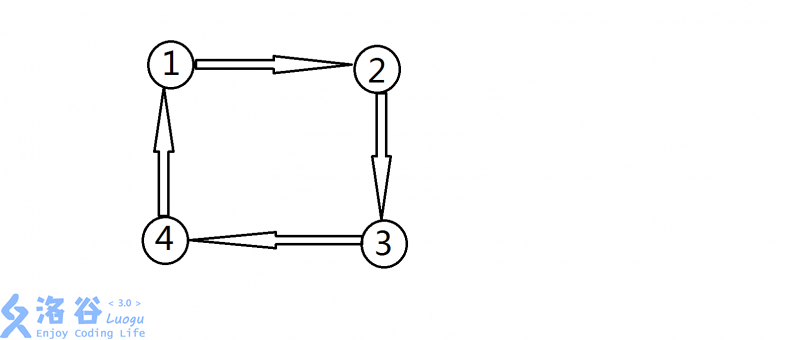
那么完成1需要完成4,完成4需要完成3，完成3需要完成2，完成2需要完成1…………诶，完成1需要完成1？这就不对了。

拓扑排序是把这种AOV网转换成一个序列（从先完成的到后完成的）的算法（相同级别谁在前谁在后随你大小便，这道题这里是关键）

再来分析一下题目

先看三个条件

1.没有平局

2.不同的球队排名不能相同

3.对于所有满足l ≤ a < b ≤ n，第a名的球队一定可以打败第b名的球队

既然a球队一定能打败b球队且a球队比b球队排名高，那么这道题就可以用拓扑，把排名高的球队指向排名低的球队，然后进行拓扑排序，就OK了。但题目还要求求出是否有多种排序方案，看上面写着这道题这里是关键的地方，如果出现了相同级别，就会出现多种排序方案，加一个判断就可以了

先看邻接矩阵的做法（这道题n ≤ 5000，不会爆空间）

#include <bits/stdc++.h>
using namespace std;
stack < int > pru;//用来存没有入度的点(名义上的起点，但不是真正的起点)，会更新，改成队列也一样 
int n, m, x, y, in[100001], out[100001], t, f, ff[5001][5001];//in[i]表示i这个点的入度，out[i]表示i这个点的出度，t存是否出现了相同级别，f存最后题目要求输出的是否有多个方案，ff[i][j]表示i这个点的第j个出度  
int main()
{
	scanf("%d %d", &n, &m);
	for(register int i = 1; i <= m; ++i)
	{
		scanf("%d %d", &x, &y);
		++in[y];
		++out[x];
		ff[x][out[x]] = y;//存出度的节点编号 
	}
	for(register int i = 1; i <= n; ++i)
	{
		if(in[i] == 0)//起点没有入度 
		{
			pru.push(i);
			++t;//有多个起点就有多个排序方案(相同级别) 
		}
	}
	if(t > 1)//多个起点 
	{
		f = 1;//存起来 
	}
	t = 0;//置零 
	while(!pru.empty())
	{
		int u = pru.top();//取出 
		pru.pop();
		printf("%d\n", u);//输出 
		t = 0;//置零 
		for(register int i = 1; i <= out[u]; ++i)//循环这个点的所有出度
		{
			int k = ff[u][i];//连出来的这个点 
			--in[k];//消除 
			if(in[k] == 0)
			{
				pru.push(k);
				++t;//相同级别 + 1 
			}
		}
		if(t > 1)//同上 
		{
			f = 1;
		}
	}
	printf("%d", f);//别忘了输出这个 
	return 0;
}

链式向前星的做法（就不写注释了，和邻接矩阵的大同小异）：

#include <bits/stdc++.h>
using namespace std;
queue < int > pru;
int n, m, head[100001], num, x, y, in[100001], t, f;
struct node
{
	int next, to;
}stu[100001];
inline void add(int x, int y)
{
	stu[++num].next = head[x];
	stu[num].to = y;
	head[x] = num;
	return;
}
int main()
{
	scanf("%d %d", &n, &m);
	for(register int i = 1; i <= m; ++i)
	{
		scanf("%d %d", &x, &y);
		add(x, y);
		++in[y];
	}
	for(register int i = 1; i <= n; ++i)
	{
		if(in[i] == 0)
		{
			pru.push(i);
			++t;
		}
	}
	if(t > 1)
	{
		f = 1;
	}
	t = 0;
	while(!pru.empty())
	{
		int u = pru.front();
		pru.pop();
		printf("%d\n", u);
		t = 0;
		for(register int i = head[u]; i; i = stu[i].next)
		{
			int k = stu[i].to;
			--in[k];
			if(in[k] == 0)
			{
				pru.push(k);
				++t;
			}
		}
		if(t > 1)
		{
			f = 1;
		}
	}
	printf("%d", f);
	return 0;
}