自动搬运

查看原文

来自洛谷，原作者为

	Believe_R_ **

搬运于2025-08-24 21:32:06，当前版本为作者最后更新于2019-08-07 19:53:10，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

一道最短路~~（？）~~的好题！！

为什么说这道题好呢？主要有以下两点：

1. 这道题完美地需要我们将点权转成边权：

$Bessie$ 需要去这么多城市，而每座城市他都要赚 $D$ 美元。那我们为什么不直接将每条普通边的边权就设置成 $D$ 呢？这两者之间是等价的呀·····

那对于飞行边来说，同理，飞行边需要花费 $T$ 美元，而到一个城市又可以赚 $D$ 美元，那我们就可以将飞行边权设为 $D-T$。

这样，存图的事就解决了

2. 只要你读懂题目，就会发现这题压根不是最短路，是最长路······

做最长路主要有两种做法（会的可以挑过，其实和做最短路的思想都一样）：

$2.1$ 做最短路是我们是现将 $dis$ 数组设为无穷大，再每次更新最小值。反过来，最长路就可以将 $dis$ 数组都设为 $0$ ,再每次更新最大值。

$2.2$ 将所有边权都取反后，再求最短路（至于为什么，在纸上画个五分钟就出来了~ $QwQ$）

如果你还不懂怎么求最长路，出门左转: 学图论，你真的了解最短路吗？

再来一道模板题：P1807 最长路_NOI导刊2010提高（07）

温馨提示：$Dijskra$ 算法无法处理负权环！

下面看我的代码，应该就看到懂了：

#include <bits/stdc++.h>
#define int long long
#define M 1000
using namespace std;

int tot=0, head[M], nex[M], to[M], dis[M];
int d, m, n, f, s;                      //d, p, c, f, s
int vis[M], w[M], cnt[M];
priority_queue<int, vector<int>, greater<int> > q;  //大根堆

inline int read()
{
    int re=0, f=1; char ch=getchar();
    while(ch<'0' || ch>'9') {if(ch=='-') f=-1; ch=getchar();}
    while(ch>='0' && ch<='9') {re=re*10+(ch-'0'); ch=getchar();}
    return re*f;
}

void add_edge(int x,int y,int z)
{
    to[++tot]=y;
    dis[tot]=z;
    nex[tot]=head[x];
    head[x]=tot;
}

void Spfa()
{
    q.push(s);
    w[s]=d; vis[s]=1; cnt[s]++;
    while(!q.empty())
    {
        int u=q.top(); q.pop();
        vis[u]=0;
        if(++cnt[u]>n) {printf("-1\n"); exit(0);}  
        for(int i=head[u];i;i=nex[i])
        {
            int v=to[i];
            if(w[v]<w[u]+dis[i])
            {
                w[v]=w[u]+dis[i];      //我是用第一种求最长路的算法做的~qwq
                if(!vis[v])
                {
                    q.push(v);
                    vis[v]=1;
                }
            }
        }
    }
}

signed main()
{
    d=read(); m=read(); n=read(); f=read(); s=read();
    for(int i=1;i<=m;++i)
    {
        int x=read(), y=read();
        add_edge(x,y,d);                      //将点权转换为边权。
    }
    for(int i=1;i<=f;++i)
    {
        int x=read(), y=read(), z=read();
        add_edge(x,y,d-z);
    }
    Spfa();
    int ans=0;
    for(int i=1;i<=n;++i) ans=max(ans,w[i]);
    printf("%lld\n",ans);
    return 0;
}

$P.s$

下面我也贴上了洛谷P1807 最长路_NOI导刊2010提高（07）的标称【这里我是用第二种求最长路的方法求的】

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=120000;
const int INF=0x3f3f3f3f;
ll dis[N],to[N],nex[N],head[N];
ll n,m,ans,tot=0;
ll d[N],vis[N];
void add_edge(int x,int y,int l)
{
    to[++tot]=y;
    dis[tot]=l;
    nex[tot]=head[x];
    head[x]=tot;
}
queue<int> q;
void Spfa()
{
    q.push(1); vis[1]=1;
    while(!q.empty())
    {
        ll u,v;
        u=q.front(); q.pop(); vis[u]=0;
        for(int i=head[u];i;i=nex[i])
        {
            v=to[i];
            if(d[v]>d[u]+dis[i])
            {
                d[v]=d[u]+dis[i];
                if(vis[v]==0) {vis[v]=1; q.push(v);}
            }
        }
    }
}
int main()
{
    scanf("%lld%lld",&n,&m);
    if(m==0) {printf("-1\n"); return 0;}
    for(int i=1;i<=m;++i)
    {
        ll x,y,l;
        scanf("%lld%lld%lld",&x,&y,&l);
        l=0-l;
        add_edge(x,y,l);              //minus
    }
    memset(d,0,sizeof(d));
    d[1]=0;
    Spfa();
    if(d[n]==0) {printf("-1\n"); return 0;}
    printf("%lld\n",-d[n]);
    return 0;
}

最后,在给大家带来一道双倍经验 $QwQ$

传送门： P2648 赚钱

大家可以自己想一下，真的和上题没什么区别！！！

不会做的请往下看：

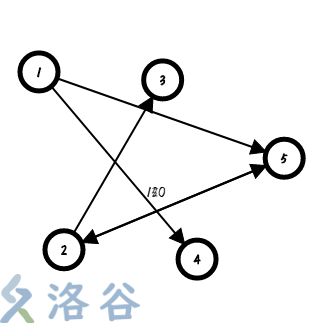
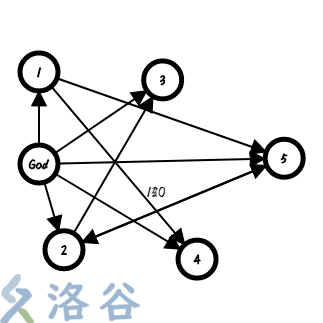
由于这题没有规定起始节点为那个，那么最简单的方法就是去枚举，然而，这复杂度不用算就知道用 $SPFA$ 肯定 $T$ 到飞！这时，我们就要引进一个超级源点。

超级源点就是在原图之外再设一个点，并将这点连向原图中所有的节点。

然后，我们从超级源点开始做 $SPFA$ ，就等同与枚举原图中的每一个节点。

在不懂就看一下这张图：

代码就看这里吧【可以尝试自己写一下】！

最后可别忘了点赞 $qwq$...